早教吧作业答案频道 -->数学-->
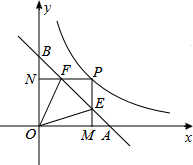
如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=kx(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为.
题目详情
如图,直线y=-x+1交x轴于A,交y轴于B,P为反比例函数y=
(x>0)上一点,PM⊥x轴于M,交AB于E,PN⊥y轴于N,交AB于F.若∠EOF=45°,则k的值为___.
| k |
| x |

▼优质解答
答案和解析
设P(a,b),则OM=a,PM=b,则点E的横坐标为a,F的纵坐标为b,
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=
=
a,AF=
=
b,
∵∠EOF=45°,
∴△AOF∽△BEO,
∴AF:BO=AO:BE,
∴AF•BE=BO•AO,
即
a•
b=1×1,
解得ab=
,
∴反比例函数y=
(x>0)中k的值为
.
故答案为:
.
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
∴△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=
| a2+(1-1+a)2 |
| 2 |
| (1-1-b)2+b2 |
| 2 |
∵∠EOF=45°,
∴△AOF∽△BEO,
∴AF:BO=AO:BE,
∴AF•BE=BO•AO,
即
| 2 |
| 2 |
解得ab=
| 1 |
| 2 |
∴反比例函数y=
| k |
| x |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
看了如图,直线y=-x+1交x轴于...的网友还看了以下:
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比 2020-05-13 …
寻高手教授数学函数迭代及如何利用桥函数解题本人愚钝,望多多指教.找位老师帮小弟一把.例题一道:求所 2020-05-16 …
设马对车的作用力为F,车对马的作用力为T,关于F与T下列说法正确的是A.F和T是一对作用力和反作用 2020-05-20 …
食物链中的数量变化关系以题为例b,c,d以a为食,e以d为食,f以e为食,g以b,c,f为食(图你 2020-05-23 …
若空气的阻力F与速度V存在这样的关系,即F=K乘*V的平方.(K为比例常数).已经知道载人舱的质量 2020-07-11 …
对应f:B到A是从集合B到A的映射吗?对于例7,如果将(3)中的对应关系f改为:每一个圆都对应它的 2020-07-12 …
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比 2020-07-24 …
为什么?SXS->S是什么?为什么要这样写!为什么能代表加法.1.二元运算的定义与实例定义10.1 2020-07-25 …
如图,正方形AOBC的边长为4,反比例函数y=k/x经过正方形的重心D点,E为AO边上任意一点,F 2020-08-01 …
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比 2020-08-03 …