将下列参数方程化为普通方程并说明它们分别表示怎样的曲线.(1)(t为参数)；(2)x=(t为参数)；(3)(t为参数).

Question

将下列参数方程化为普通方程并说明它们分别表示怎样的曲线.

(1) 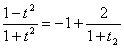(t为参数)；(2)x= 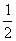(t为参数)；

(3) 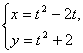(t为参数).

Answer 1

思路分析：本题所给的题目中所体现的方法都是常见的一些将曲线的参数方程化为普通方程的方法 对于具体的将参数方程转化为普通方程的题目要视具体题目而去选择消去参数的方式.

（1）由x=cos ² t=1-sin ² t=1-y ² 知y ² =-(x-1).由x=cos ² t 可知0≤x≤1.故其普通方程为y ² =-(x-1)(0≤x≤1) 它表示的是以点(1 0)为顶点、开口向左的一条抛物线上的一段.

（2）将两式平方相加 得x ² +y ² =1.由x= 得x≠-1.故其普通方程为x ² +y ² =1(x≠-1) 它表示以原点为圆心、1为半径的圆（除去与x轴相交的左交点）.

（3）将两式相减 得t= (y-x-2).代入第二个方程 整理得x ² -2xy+y ² +4x-8y+12=0.