早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.(1)证明:GF=CE.(2)试求五边形ABCFE的面积.
题目详情
如图,已知正方形ABCD的边长为2,在CD的延长线上取一点E,以CE为直径作圆交AD的延长线于点F,连接FB交圆于另一点G,且GB=DF.
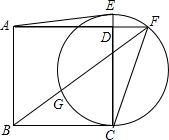
(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.

(1)证明:GF=CE.
(2)试求五边形ABCFE的面积.
▼优质解答
答案和解析
(1)证明:连接AG,GH,
∵正方形ABCD,
∴∠BCD=∠ADC=90°,AB=BC,
∵CE为圆的直径,
∴BC是圆的切线,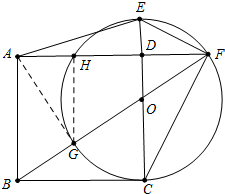
∴BC2=BG•BF,
∴AB2=BG•BF,
∴
=
,
∵∠ABG=∠FBA,
∴△ABG∽△FBA,
∴∠AGB=∠BAF=90°,
∴AG2=AB2-BG2=AD2-DF2=(AD+DF)(AD-DF)=AF(AD-AF),
∵CE为圆的直径,∠ADC=90°,
∴DF=DH,
∴AG2=AF•AH,
∴
=
,
∵∠FAG=∠GAH,
∴△AGH∽△AFG,
∴∠AHG=∠AGF=90°,
∴FG是圆的直径,
∴FG=CE;
(2) 设BG=DF=DH=x,圆的半径为R,则BF=x+2R,AF=2+x,DE=2R-2,由勾股定理和相交弦定理得到,
BO2=CB2+CO2,CD•DE=DF•DH,
∴(x+R)2=R2+22,2(2R-2)=x2,
∴x2+2xR=4,4R-4=x2,
∴4R-4+2xR=4,
∴4R+2xR=8,
∴2R+xR=4,
∴S五边形ABCFE=S正方形ABCD+S△ADE+S△ECF=2+2R+xR=2+4=6.
∵正方形ABCD,
∴∠BCD=∠ADC=90°,AB=BC,
∵CE为圆的直径,
∴BC是圆的切线,

∴BC2=BG•BF,
∴AB2=BG•BF,
∴
| AB |
| BF |
| BG |
| AB |
∵∠ABG=∠FBA,
∴△ABG∽△FBA,
∴∠AGB=∠BAF=90°,
∴AG2=AB2-BG2=AD2-DF2=(AD+DF)(AD-DF)=AF(AD-AF),
∵CE为圆的直径,∠ADC=90°,
∴DF=DH,
∴AG2=AF•AH,
∴
| AG |
| AF |
| AH |
| AG |
∵∠FAG=∠GAH,
∴△AGH∽△AFG,
∴∠AHG=∠AGF=90°,
∴FG是圆的直径,
∴FG=CE;
(2) 设BG=DF=DH=x,圆的半径为R,则BF=x+2R,AF=2+x,DE=2R-2,由勾股定理和相交弦定理得到,
BO2=CB2+CO2,CD•DE=DF•DH,
∴(x+R)2=R2+22,2(2R-2)=x2,
∴x2+2xR=4,4R-4=x2,
∴4R-4+2xR=4,
∴4R+2xR=8,
∴2R+xR=4,
∴S五边形ABCFE=S正方形ABCD+S△ADE+S△ECF=2+2R+xR=2+4=6.
看了 如图,已知正方形ABCD的边...的网友还看了以下:
已知以点O为公共圆心的两个同心圆,大圆的弦交小圆于C,D两点,如果AB=6cm,CD=4cm,求圆 2020-04-25 …
点A,B,C,D分别是蛋圆与坐标轴的焦点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心 2020-04-26 …
一圆弧拱桥圆心为o,跨度为7.2米,过o作oc垂直于AB于D,交圆弧于C,CD=2.4米,一宽3米 2020-04-27 …
在场强为E的匀强电场中,取O点为圆心,r为半径作一圆周,在O点固定一电荷量为+Q的点电荷,a、b、 2020-05-13 …
如图所示,在半径为R的圆周上的六个等分点分别为C、D、E、F、G、H,其中以D、E、G、H为圆心、 2020-05-17 …
O'在圆O上,以O'为圆心的圆交O'于A,B,圆O的弦O'C交圆O;于D,求证D为三角形abc内心 2020-06-02 …
直线与圆2(818:26:25)已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上,且与圆C外切 2020-06-03 …
如图,圆O与圆D相交于A,B两点,BC为圆D的切线,点C在圆O上,且AB=BC.(1)证明:点O在 2020-06-09 …
如图,半径为1圆心角为3π2圆弧AB上有一点C.(1)当C为圆弧AB中点时,D为线段OA上任一点, 2020-06-11 …
谁能解这道数学题啊已知圆C:(x+4)2+y2=4.圆D的圆心D在y轴上且与圆C外切.圆D与y轴交 2020-06-14 …