早教吧作业答案频道 -->数学-->
已知直线l:y=x+1与曲线C:交于不同的两点A,B,O为坐标原点.(Ⅰ)若|OA|=|OB|,求证:曲线C是一个圆;(Ⅱ)若OA⊥OB,当a>b且时,求曲线C的离心率e的取值范围.
题目详情
已知直线l:y=x+1与曲线C: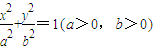 交于不同的两点A,B,O为坐标原点.
交于不同的两点A,B,O为坐标原点.
(Ⅰ)若|OA|=|OB|,求证:曲线C是一个圆;
(Ⅱ)若OA⊥OB,当a>b且 时,求曲线C的离心率e的取值范围.
时,求曲线C的离心率e的取值范围.
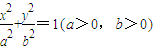 交于不同的两点A,B,O为坐标原点.
交于不同的两点A,B,O为坐标原点.(Ⅰ)若|OA|=|OB|,求证:曲线C是一个圆;
(Ⅱ)若OA⊥OB,当a>b且
 时,求曲线C的离心率e的取值范围.
时,求曲线C的离心率e的取值范围.▼优质解答
答案和解析
【答案】分析:(Ⅰ)设直线L与曲线C的交点利用两点间的距离公式和题设等式求得x12-x22=y22-y12,把A,B代入椭圆的方程两式相减求得整理求得a和b的关系,判断出曲线的图象是圆.(Ⅱ)设直线L与曲线C的交点根据a>b判断出曲线C为椭圆,根据OA⊥OB判断出两直线的斜率之积为-1,求得y1y2=-x1x2,将y=x+1代入椭圆的方程,利用韦达定理求得x1+x2和x1x2的表达式,进而利用直线方程求得y1y2的表达式,进而建立等式求得关于a和c的方程,求得a和c的关系式,进而表示出椭圆的离心率,利用a的范围确定离心率的范围.(Ⅰ)证明:设直线L与曲线C的交点为A(x1,y1)B(x2,y2)∵|OA|=|OB|∴即:x12+y12=x22+y22∴x12-x22=y22-y12∵A,B在C上∴,∴两式相减得:∴即:a2=b2∴曲线C是一个圆(Ⅱ)设直线L与曲线C的交点为A(x1,y1)B(x2,y2),∵a>b>o∴曲线C是焦点在x轴上的椭圆∵OA⊥OB∴即:y1y2=-x1x2将y=x+1代入b2x2+a2y2-a2b2=0整理得:(b2+a2)x2+2a2+a2-a2b2=0∴,∵A,B在L上∴y1y2=(x1+1)(x2+1)=x1•x2+x2+x1+1又∵y1y2=-x1x2∴2x1x2+x2+x1+1=0∴2∴b2+a2-2b2a2=0∴a2+a2-c2-2a2(a2-c2)=0∴2a4-2a2+c2-2c2a2=0∴∴∵∴2a2-1∈[2,4]∴点评:本题主要考查了直线与圆锥曲线的综合问题,椭圆的基本性质.要求考生能对椭圆中a,b和c的关系能熟练理解和应用.
看了 已知直线l:y=x+1与曲线...的网友还看了以下:
高数极限证明在极限证明中,可以取任意最小值,但是如果,一道题的极限本来等于1,就算是我把他错当成2 2020-05-13 …
关于x的方程mx旳平方+4x+1=0有两个不相等的实数根,则m时取值范围是 2020-05-15 …
已知抛物线y=-x+ax+1/2与直线y=2x(1)求证:抛物线与直线相交;(2)当抛物线的顶点在 2020-05-20 …
等比数列问题.在用配凑法求等比数列时,取值范围有点晕~例如,若已知b1=2,且得到了这个式子:bn 2020-07-14 …
确定常数a,b使x趋近于0时.f(x)=(a+bcosx)sinx-x为x的5阶无穷小答案是a=4 2020-07-15 …
设函数f(x)=lnx+x2+ax.(Ⅰ)若时,f(x)取得极值,求a的值;(Ⅱ)若f(x)在其定 2020-07-20 …
(本小题满分13分)设函数(I)若当时,取得极值,求的值,并讨论的单调性;(II)若存在极值,求的 2020-07-31 …
还是一次函数确定1个函数解析式自变量的取值范围,就是要保证这个关系式有意义,具体地说,当关系式昰只含 2020-11-07 …
抽象函数为什么对应关系相同时取值范围一致?看抽象函数定义域的题总有一个重点是“同一对应关系下括号内范 2020-12-17 …
计算标准差时,取值n和n-1有什么区别? 2021-01-01 …