求棱长为1的正四面体的外接球、内切球的表面积．

Question

求棱长为1的正四面体的外接球、内切球的表面积．

Answer 1

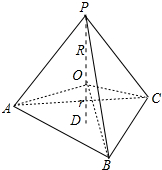设正四面体为PABC，两球球心重合，设为O．
设PO的延长线与底面ABC的交点为D，则PD为正四面体PABC的高，PD⊥底面ABC，且PO=R，OD=r，OD=正四面体PABC内切球的高．
设正四面体PABC底面面积为S．
将球心O与四面体的4个顶点PABC全部连接，
可以得到4个全等的正三棱锥，球心为顶点，以正四面体面为底面．
每个正三棱锥体积V₁=(1)/(3)•S•r 而正四面体PABC体积V₂=(1)/(3)•S•（R+r）
根据前面的分析，4•V₁=V₂，
所以，4•(1)/(3)•S•r=(1)/(3)•S•（R+r），
所以，R=3r，
因为棱长为1，所以AD=(√(3))/(3)，
所以PD=(√(6))/(3)，
所以R=(√(6))/(4)，r=(√(6))/(12)
所以棱长为1的正四面体的外接球为4π•（(√(6))/(4)）²=(3)/(2)π、内切球的表面积为4π•（(√(6))/(12)）²=(π)/(6)．