早教吧作业答案频道 -->数学-->
将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接CD.(1)连接BD,①如图1,若α=80°,则∠BDC的度数为;②在第二次旋转过程中,请探究∠BD
题目详情
将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接CD.
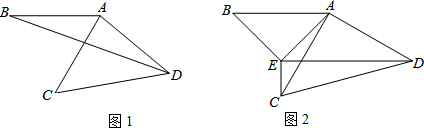
(1)连接BD,
①如图1,若α=80°,则∠BDC的度数为___;
②在第二次旋转过程中,请探究∠BDC的大小是否改变.若不变,求出∠BDC的度数;若改变,请说明理由.
(2)如图2,以AB为斜边作直角三角形ABE,使得∠B=∠ACD,连接CE,DE.若∠CED=90°,求α的值.

(1)连接BD,
①如图1,若α=80°,则∠BDC的度数为___;
②在第二次旋转过程中,请探究∠BDC的大小是否改变.若不变,求出∠BDC的度数;若改变,请说明理由.
(2)如图2,以AB为斜边作直角三角形ABE,使得∠B=∠ACD,连接CE,DE.若∠CED=90°,求α的值.
▼优质解答
答案和解析
(1)①∵线段AC,AD由AB旋转而成,
∴AB=AC=AD.
∴点B、C、D在以A为圆心,AB为半径的圆上.
∴∠BDC=
∠BAC=30°.
故答案为:30°.
②不改变,∠BDC的度数为30°.
方法一:
由题意知,AB=AC=AD.
∴点B、C、D在以A为圆心,AB为半径的圆上.
∴∠BDC=
∠BAC=30°.
方法二:
由题意知,AB=AC=AD.
∵AC=AD,∠CAD=α,
∴∠ADC=∠C=
=90°-
α.
∵AB=AD,∠BAD=60°+α,
∴∠ADB=∠B=
=
=60°-
α.
∴∠BDC=∠ADC-∠ADB=(90°-
α)-(60°-
α)=30°.
(2)过点AM⊥CD于点M,连接EM.
∵∠AMD=90°,
∴∠AMC=90°.
在△AEB与△AMC中,
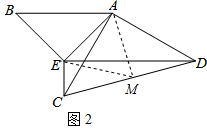 ,
,
∴△AEB≌△AMC(AAS).
∴AE=AM,∠BAE=∠CAM.
∴∠EAM=∠EAC+∠CAM=∠EAC+∠BAE=∠BAC=60°.
∴△AEM是等边三角形.
∴EM=AM=AE.
∵AC=AD,AM⊥CD,
∴CM=DM.
又∵∠DEC=90°,
∴EM=CM=DM.
∴AM=CM=DM.
∴点A、C、D在以M为圆心,MC为半径的圆上.
∴α=∠CAD=90°.
∴AB=AC=AD.
∴点B、C、D在以A为圆心,AB为半径的圆上.
∴∠BDC=
| 1 |
| 2 |
故答案为:30°.
②不改变,∠BDC的度数为30°.
方法一:
由题意知,AB=AC=AD.
∴点B、C、D在以A为圆心,AB为半径的圆上.
∴∠BDC=
| 1 |
| 2 |
方法二:
由题意知,AB=AC=AD.
∵AC=AD,∠CAD=α,
∴∠ADC=∠C=
| 180°-α |
| 2 |
| 1 |
| 2 |
∵AB=AD,∠BAD=60°+α,
∴∠ADB=∠B=
| 180°-(60°+α) |
| 2 |
| 180°-α |
| 2 |
| 1 |
| 2 |
∴∠BDC=∠ADC-∠ADB=(90°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点AM⊥CD于点M,连接EM.
∵∠AMD=90°,
∴∠AMC=90°.
在△AEB与△AMC中,
|
 ,
,∴△AEB≌△AMC(AAS).
∴AE=AM,∠BAE=∠CAM.
∴∠EAM=∠EAC+∠CAM=∠EAC+∠BAE=∠BAC=60°.
∴△AEM是等边三角形.
∴EM=AM=AE.
∵AC=AD,AM⊥CD,
∴CM=DM.
又∵∠DEC=90°,
∴EM=CM=DM.
∴AM=CM=DM.
∴点A、C、D在以M为圆心,MC为半径的圆上.
∴α=∠CAD=90°.
看了 将线段AB绕点A逆时针旋转6...的网友还看了以下:
已知函数y=ln(x-5),在x=5处,函数()A.连续可导B.连续不可导C已知函数y=ln(x- 2020-05-14 …
在Excel中可选取( )单元格。 A.单个 B.多个 C.连续 D.不连续 2020-05-19 …
一道高数函数连续性的问题!谢谢!设f(x)在x0连续,g(x)在x0不连续,则在x0处()A.f( 2020-06-06 …
在浇筑地下连续墙时,连接两相邻单元墙段,当前应用最多的方法是( )。 A.修筑导墙B.泥浆护 2020-06-07 …
在浇筑地下连续墙时,连接两相邻单元墙段,当前应用最多的方法是( )。 A.修筑导墙 B.泥 2020-06-07 …
怎么证明是光滑曲线!我快疯了!说是得一阶连续导数,连续,一元函数连续定义我懂,可又来了个连续的时候 2020-06-18 …
当x不等于0时,函数f(x)=xsin(1/x);当x等于0时,函数f(x)=0,则在x=0处()A 2020-11-03 …
、数字信号的特征是().数字信号的特征是().(A)时间上连续幅值上离散(B)时间上离散幅值上连续( 2020-11-17 …
1函数f[x]在xo处可导,则|f[x]|在xo处A必定可导B必定不可导C必定连续D必定不连续2函数 2020-11-20 …
线性表若采用链表存储结构,要求内存中可用存储单元地址?A、必须连续B、部分地址必须连续C、一定不连续 2020-12-28 …