早教吧作业答案频道 -->数学-->
等腰△ABC,△DCE中,∠BAC+∠CDE=180°,AB=AC,DC=DE,连接BE,取BE的中点P,连接PA,PD.①如图1,当∠BAC=∠CDE=90°时,猜想并验证PA与PD的数量关系和位置关系.②如图2,当∠BAC≠∠CDE≠90°时,
题目详情
等腰△ABC,△DCE中,∠BAC+∠CDE=180°,AB=AC,DC=DE,连接BE,取BE的中点P,连接PA,PD.
①如图1,当∠BAC=∠CDE=90°时,猜想并验证PA与PD的数量关系和位置关系.
②如图2,当∠BAC≠∠CDE≠90°时,猜想并验证PA与PD的位置关系.
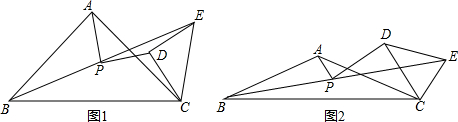
①如图1,当∠BAC=∠CDE=90°时,猜想并验证PA与PD的数量关系和位置关系.
②如图2,当∠BAC≠∠CDE≠90°时,猜想并验证PA与PD的位置关系.

▼优质解答
答案和解析
 ①PA=PD且PA⊥PD,理由是:
①PA=PD且PA⊥PD,理由是:
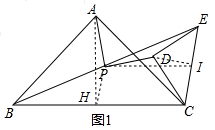
如图1,取BC的中点H,CE的中点I,连接AH、PH、PI、DI,
∵∠BAC=∠CDE=90°,AB=AC,DC=DE,
∴△ABC和△CDE是等腰直角三角形,
∴AH⊥BC,DI⊥CE,
∴∠AHC=∠DIC=90°,
∵P、H、I分别是BE、BC、EC的中点,
∴PH、PI是△BEC的中位线,AH=
BC=CH,DI=
BC=CI
∴PH∥EC,PI∥BC,
∴四边形PHCI是平行四边形,
∴PH=CI,PI=CH,∠PHC=∠PIC,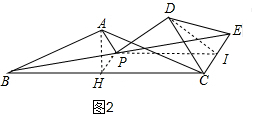 ∴AH=PI,∠AHP=∠PID,PH=DI,
∴AH=PI,∠AHP=∠PID,PH=DI,
∴△AHP≌△PID,
∴AP=PD,∠HAP=∠DPI,
∵∠HAP+∠APH+∠AHP+∠AHB=180°+90°=270°,
∴∠HAP+∠APH+∠PHB=270°,
∴∠DPI+APH+∠IPH=270°,
∴∠APD=360°-270°=90°,
∴PA⊥PD;
(2)如图2,AP⊥PD,理由是:
取BC的中点H,EC的中点I,连接AH、PH、PI、DI,
同理可得:四边形PHCI是平行四边形,
∴PI=CH,PH=CI,
∵AB=AC,H是BC的中点,
∴AH平分∠BAC,AH⊥BC,
∴∠HAC=
∠BAC,∠AHC=90°,
同理,∠CDI=
∠CDE,∠DIC=90°,
∵∠BAC+∠CDE=180°,
∴∠HAC+∠CDI=90°,
∵∠HAC+∠HCA=90°,
∴∠CDI=∠HCA,
∵∠AHC=∠DIC=90°,
∴△AHC∽△CID,
∴
=
,
∴
=
,
∵∠AHC=∠DHI,∠PHC=∠PIC,
∴∠AHC-∠PHC=∠DIC-∠PIC,
即∠AHP=∠DIP,
∴△AHP∽△PID,
∴∠HAP=∠DPI,
∵∠APH+∠HAP+∠AHP+∠AHB=180°+90°=270°,
∴∠HAP+∠APH+∠PHB=270°,
∵PI∥BC,
∴∠PHB=∠HPI,
∴∠DPI+∠APH+∠HPI=270°,
∵∠DPI+∠APH+∠HPI+∠APD=360°,
∴∠APD=90°,
∴AP⊥PD.
 ①PA=PD且PA⊥PD,理由是:
①PA=PD且PA⊥PD,理由是:如图1,取BC的中点H,CE的中点I,连接AH、PH、PI、DI,
∵∠BAC=∠CDE=90°,AB=AC,DC=DE,
∴△ABC和△CDE是等腰直角三角形,
∴AH⊥BC,DI⊥CE,
∴∠AHC=∠DIC=90°,
∵P、H、I分别是BE、BC、EC的中点,
∴PH、PI是△BEC的中位线,AH=
| 1 |
| 2 |
| 1 |
| 2 |
∴PH∥EC,PI∥BC,
∴四边形PHCI是平行四边形,
∴PH=CI,PI=CH,∠PHC=∠PIC,
 ∴AH=PI,∠AHP=∠PID,PH=DI,
∴AH=PI,∠AHP=∠PID,PH=DI,∴△AHP≌△PID,
∴AP=PD,∠HAP=∠DPI,
∵∠HAP+∠APH+∠AHP+∠AHB=180°+90°=270°,
∴∠HAP+∠APH+∠PHB=270°,
∴∠DPI+APH+∠IPH=270°,
∴∠APD=360°-270°=90°,
∴PA⊥PD;
(2)如图2,AP⊥PD,理由是:
取BC的中点H,EC的中点I,连接AH、PH、PI、DI,
同理可得:四边形PHCI是平行四边形,
∴PI=CH,PH=CI,
∵AB=AC,H是BC的中点,
∴AH平分∠BAC,AH⊥BC,
∴∠HAC=
| 1 |
| 2 |
同理,∠CDI=
| 1 |
| 2 |
∵∠BAC+∠CDE=180°,
∴∠HAC+∠CDI=90°,
∵∠HAC+∠HCA=90°,
∴∠CDI=∠HCA,
∵∠AHC=∠DIC=90°,
∴△AHC∽△CID,
∴
| AH |
| CI |
| CH |
| DI |
∴
| AH |
| PH |
| PI |
| DI |
∵∠AHC=∠DHI,∠PHC=∠PIC,
∴∠AHC-∠PHC=∠DIC-∠PIC,
即∠AHP=∠DIP,
∴△AHP∽△PID,
∴∠HAP=∠DPI,
∵∠APH+∠HAP+∠AHP+∠AHB=180°+90°=270°,
∴∠HAP+∠APH+∠PHB=270°,
∵PI∥BC,
∴∠PHB=∠HPI,
∴∠DPI+∠APH+∠HPI=270°,
∵∠DPI+∠APH+∠HPI+∠APD=360°,
∴∠APD=90°,
∴AP⊥PD.
看了 等腰△ABC,△DCE中,∠...的网友还看了以下:
若只通过测定装置中C、D的增重来确定x,则装置按气流方向接口的连接顺序为()A.a→b→c→eB. 2020-05-17 …
下列说法中正确的是()A.现在使用的移动电话有发射装置和接收装置B.现在使用的对讲机有发射装置和接 2020-05-17 …
有A、B、C、D4种装置,将1个数输入一种装置后会输出另1个数.装置A:将输入的数加上5;装置B: 2020-06-16 …
有A、B、C、D四种计算装置,装置A:将输入的数乘以5;装置B:将输入的数加3;装置c:将输入的数 2020-06-16 …
有A、B、C、D4种装置,将1个数输入一种装置后会输出另1个数.装置A:将输入的数加上5;装置B: 2020-06-16 …
有A、B、C、D4种装置,将1个数输入一种装置后会输出另1个数.装置A:将输入的数加上5;装置B: 2020-06-16 …
有A,B,C,D四种计算装置,装置A:将输入的数乘以5;装置B:将输入的数加3;装置C:将输入的数 2020-06-16 …
关于高压三芯电缆合并做一相高压电缆ZR-YJV8.7/10KV3x(3x300).由于A.B.C接 2020-06-21 …
一、在正方形网格内有∠AOB,请你利用网格化出∠AOB的平分线,并说明理由二、把△ABC饶点A旋转至 2020-10-31 …
已知三角形ABC的面积为根号3.角A.B.C所对的边分别是a.b.c.(接下)(连上)且sin的平方 2021-02-07 …