早教吧作业答案频道 -->数学-->
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=2(1)求证:B1C∥平面A1BM(2)求证:平面AC1B1⊥平面A1BM.
题目详情
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=
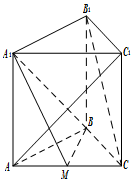
(1)求证:B1C∥平面A1BM
(2)求证:平面AC1B1⊥平面A1BM.
| 2 |

(1)求证:B1C∥平面A1BM
(2)求证:平面AC1B1⊥平面A1BM.
▼优质解答
答案和解析
证明:(1)连接AB1交A1B于O,连接OM.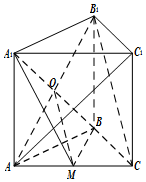
在△B1AC中,∵M,O分别为AC,AB1的中点,
∴OM∥B1C.
又∵OM⊂平面A1BM,B1C⊄平面A1BM,
∴B1C∥平面A1BM.
(2)∵侧棱AA1⊥底面ABC,BM⊂平面ABC,∴AA1⊥BM.
又∵M为棱AC中点,AB=BC,∴BM⊥AC.
∵AA1∩AC=A,∴BM⊥平面ACC1A1.
∴BM⊥AC1.
∵M为棱AC中点,AC=2,∴AM=1.
又∵AA1=
,∴在RT△ACC1和RT△A1AM中,
tan∠ACC1=tan∠A1MA=
,
∴∠ACC1=∠A1MA,
即∠ACC1+∠C1AC=∠A1MA+∠C1AC=90°,.
∴A1M⊥AC1.∵BM∩A1M=M,
∴AC1⊥平面A1BM.AC1⊂平面AC1B1
平面AC1B1⊥平面A1BM.

在△B1AC中,∵M,O分别为AC,AB1的中点,
∴OM∥B1C.
又∵OM⊂平面A1BM,B1C⊄平面A1BM,
∴B1C∥平面A1BM.
(2)∵侧棱AA1⊥底面ABC,BM⊂平面ABC,∴AA1⊥BM.
又∵M为棱AC中点,AB=BC,∴BM⊥AC.
∵AA1∩AC=A,∴BM⊥平面ACC1A1.
∴BM⊥AC1.
∵M为棱AC中点,AC=2,∴AM=1.
又∵AA1=
| 2 |
tan∠ACC1=tan∠A1MA=
| 2 |
∴∠ACC1=∠A1MA,
即∠ACC1+∠C1AC=∠A1MA+∠C1AC=90°,.
∴A1M⊥AC1.∵BM∩A1M=M,
∴AC1⊥平面A1BM.AC1⊂平面AC1B1
平面AC1B1⊥平面A1BM.
看了 如图,在三棱柱ABC-A1B...的网友还看了以下:
41.要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面. 2020-04-27 …
小丽参加课外兴趣小组活动时,设计了一个圆柱体模型,现有150张白纸,一张白纸可做侧面16个,或做底 2020-07-17 …
如图,四棱锥P-ABCD的底面是AB=2,BC=2的矩形,侧面PAB是等边三角形,且侧面PAB⊥底 2020-07-20 …
三棱锥三条侧棱两两垂直,三个侧面与底面所成二面角分别为30°、45°、60°,底面积为1,则此三棱 2020-07-31 …
若正三棱柱(侧棱垂直于底面,且底面为正三角形)的两个侧面的异面对角线互相垂直,则它的底面边长与侧棱 2020-07-31 …
在某条街道上,沿街店面的门牌号码是这样的:在街道一侧从1开始,依次用连续的奇数排号:对面的一侧用连续 2020-11-08 …
现在有150张白纸,一张白纸可做侧面16个,或者做底面43个,1个侧面与2个底面配成一套模型,问用多 2020-11-15 …
一个正方体的六个面分别写着1,2,3,4,5,6六个数,三个人从不同的角度看到的结果如下.第一个:上 2020-11-17 …
1.一个圆柱,底面半径1分米,它的侧面展开是一个正方形,它的高是多少分米?它的侧面积是多少平方分米? 2020-12-02 …
已知四棱锥P-ABCD中,底面ABCD为正方形,PC⊥平面ABCD,AB=1,PC=2,E为侧棱PC 2020-12-23 …