早教吧作业答案频道 -->数学-->
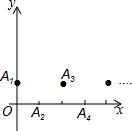
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0
题目详情
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.
(1)找规律:C1的对称轴为x=___,C2的对称轴为x=___;并直接写出抛物线C3、C4的解析式.
(2)若点E(e,f1)、F(e,f2)分别在抛物线C27、C28上,当e=30时,求线段EF的长.
(3)若直线x=m分别交x轴、抛物线C999、抛物线C1000于点P、M、N,作直线A1000M、A1000N,当∠PA1000M=45°时,求sin∠PA1000M的值.

(1)找规律:C1的对称轴为x=___,C2的对称轴为x=___;并直接写出抛物线C3、C4的解析式.
(2)若点E(e,f1)、F(e,f2)分别在抛物线C27、C28上,当e=30时,求线段EF的长.
(3)若直线x=m分别交x轴、抛物线C999、抛物线C1000于点P、M、N,作直线A1000M、A1000N,当∠PA1000M=45°时,求sin∠PA1000M的值.
▼优质解答
答案和解析
(1)∵A1(0,1)、A2(1,0)、A3(2,1)
∴A1(0,1)、A3(2,1)关于x=1对称,
∴C1的对称轴为x=1,
同理C2的对称轴为x=2,
故答案为1,2;
由顶点式求出C3的解析式为:y=(x-3)2,C4的解析式为:y=-(x-4)2+1.
(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
∴当e=30时,f1=(30-27)2=9,f2=(30-28)2+1=5,
∴EF=f1-f2=4.
(3)由(2)中发现的规律可知,抛物线C999、C1000解析式分别为:y=(x-999)2,
y=-(x-1000)2+1.
点A1000坐标为(999,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图
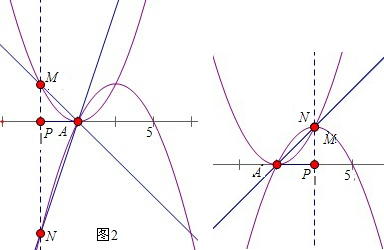
在A1000(999,0)点左侧,当m=998时,M(998,1)此时有∠PA1000M=45°,N(998,-3),相应的sin∠PA1000N的值为
;
在A1000(999,0)点右侧,当m=1000时,M(1000,1)此时有∠PA1000M=45°,N(1000,1),相应的sin∠PA1000N的值为
.
∴A1(0,1)、A3(2,1)关于x=1对称,
∴C1的对称轴为x=1,
同理C2的对称轴为x=2,
故答案为1,2;
由顶点式求出C3的解析式为:y=(x-3)2,C4的解析式为:y=-(x-4)2+1.
(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
∴当e=30时,f1=(30-27)2=9,f2=(30-28)2+1=5,
∴EF=f1-f2=4.
(3)由(2)中发现的规律可知,抛物线C999、C1000解析式分别为:y=(x-999)2,
y=-(x-1000)2+1.
点A1000坐标为(999,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图

在A1000(999,0)点左侧,当m=998时,M(998,1)此时有∠PA1000M=45°,N(998,-3),相应的sin∠PA1000N的值为
3
| ||
| 10 |
在A1000(999,0)点右侧,当m=1000时,M(1000,1)此时有∠PA1000M=45°,N(1000,1),相应的sin∠PA1000N的值为
| ||
| 2 |
看了 如图,在平面直角坐标系中,有...的网友还看了以下:
10的n(n为正整数)此方的结果中0的个数等于0,那么0.1的n(n为正整数)次方的结果有什么规律 2020-05-14 …
已知抛物线y=-x的平方+bx+c与x轴的两个交点分别为A(m,0),B(n,0),且m+n=4, 2020-05-23 …
已知a=2,你能说明a是无理数吗?设a=n/m,m与n是互质的已知a=2,你能说明a是无理数吗?设 2020-05-24 …
在任意两个非零实数ab中插入n个数使其构成等比数列若ab>0则n∈N+如果q大于0那么数列的所有项 2020-06-03 …
已知抛物线y=一x2+bx+c与x轴的两仑交点分别为A(m,0),B(n,0),且m十n=4,n分 2020-07-02 …
有这个根号内A的M次的N次根,MN都要属于N+.且A要大于0,还有N大于1.我现在可以拿出这个:- 2020-07-18 …
求关于x的方程x[(x-1)^n-1]/(x-2)=0所有解.答案好像是x=0或x=e^(i*2k 2020-07-31 …
若多项式f(x)的导数等于0的方程(即f'(x)=0)有n-1个重根:x=a,则方程f(x)-f( 2020-07-31 …
在任意两个非零实数ab中插入n个数使其构成等比数列若ab>0则n∈N+如果q大于0那么数列的所有项的 2020-11-18 …
[辨析]这道题错在哪儿?已知当x→0时3x-4sinx+sinxcosx与x^n同阶无穷小,则n=? 2020-12-17 …