早教吧作业答案频道 -->数学-->
如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.(1)求证:CF=EB.(2)若AB=12,AF=8,求CF的长.
题目详情
如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
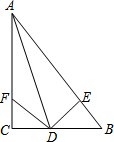
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.

(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
▼优质解答
答案和解析
(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
∵
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2) 设CF=x,则AE=12-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在△ACD与△AED中,
∵
,
∴△ACD≌△AED(HL),
∴AC=AE,即8+x=12-x,
解得x=2,即CF=2.
∴DE=DC.
在△CDF与△EDB中,
∵
|
∴Rt△CDF≌Rt△EDB(HL),

∴CF=EB.
(2) 设CF=x,则AE=12-x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在△ACD与△AED中,
∵
|
∴△ACD≌△AED(HL),
∴AC=AE,即8+x=12-x,
解得x=2,即CF=2.
看了 如图,在△ABC中,AD平分...的网友还看了以下:
高一函数填空题知幂函数y=f(x)的图像过点(2,根号2),则f(9)=若f(x)是一次函数,f( 2020-05-13 …
已知FX=A(SINX绝对值+COSX绝对值)+4SIN2X+9,若F(9派/4)=13-9根号2 2020-06-11 …
已知函数f(x)=m•2x+2•3x,m∈R.(1)当m=-9时,求满足f(x+1)>f(x)的实 2020-06-12 …
已知点E(x,1)F(9,y),若EF平行y轴,则x,y已知点E(x,1)F(9,y),若EF平行 2020-06-29 …
若f(n)为n2+1的各位数字之和(n∈N*),例如:∵142+1=197,1+9+7=17,∴f 2020-07-18 …
高一数学,求高手,急!(1)已知幂函数y=f(x)的图象过点(2,根号2),则f(9)=.是不是就 2020-08-01 …
已知函数f(x)的导函数f'(x)是二次函数,且f'(x)=0的两根为±1.若f(x)的极大值与极 2020-08-01 …
已知函数f(x)的导函数f'(x)是二次函数,且f'(x)=0的两根为±1.若f(x)的极大值与极 2020-08-01 …
若f(小)在(-9,9)内可微,且f′(0)=0,f″(0)=A存在,则极限li5小→0f(小)−f 2020-11-03 …
f(x+3)+f(3)=f(3x+9)这是世纪金榜的题目我想问这个为什么相等请专业人士,详细回答本人 2020-11-14 …