如图1，在平行四边形ABCD中，AB=2AD，E，F分别为AB，CD的中点，沿EF将四边形AEFD折起到新位置变为四边形A′EFD′，使A′B=A′F（如图2所示）．（1）证明：A′E⊥BF；（2）若∠BAD=60°，A′E=2A&apos

Question

如图1，在平行四边形ABCD中，AB=2AD，E，F分别为AB，CD的中点，沿EF将四边形AEFD折起到新位置变为四边形A′EFD′，使A′B=A′F（如图2所示）．

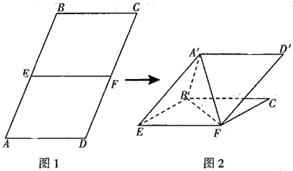
（1）证明：A′E⊥BF；
（2）若∠BAD=60°，A′E=√(2)A'B=2，求多面体A′BE-D′CF的体积．

Answer 1

证明：（1）取BF的中点O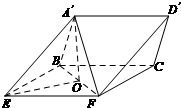，连接A'O，EO，
∵A'B=A'F，BE=EF，
∴BF⊥A'O，BF⊥EO，
又A′O⊂平面A′OE，OE⊂平面A′OE，A'O∩EO=O，
∴BF⊥平面A'EO，∵A'E⊂平面A'EO，
∴A'E⊥BF．   
（2）∵BE=EF=2，∠BEF=60°，
∴BF=2，EO=√(3)，
∵A′E=√(2)A′B=2，∴A′B=A′F=√(2)，
∵A′O⊥BF，∴A'O=1，
∴A′O²+OE²=A′E²，
∴A'O⊥EO，又A′O⊥BF，
∴A'O⊥平面BEF，
∴VA′-BEF=(1)/(3)×(1)/(2)×2×2×sin60°=(√(3))/(3)，
∴VA′BE-D′FC=3VA′-BEF=√(3)．