早教吧作业答案频道 -->数学-->
如图1,在平面直角坐标系中,点A的坐标为(-4,4),点B的坐标为(0,2).(1)求直线AB的解析式;(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点
题目详情
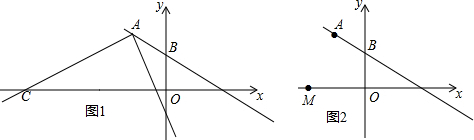
如图1,在平面直角坐标系中,点A的坐标为(-4,4),点B的坐标为(0,2).
(1)求直线AB的解析式;
(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点D.当∠CAD绕着点A旋转时,OC-OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M(-4,0)是x轴上的一个点,点P是坐标平面内一点.若A、B、M、P四点能构成平行四边形,请写出满足条件的所有点P的坐标(不要解题过程).
(1)求直线AB的解析式;
(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点D.当∠CAD绕着点A旋转时,OC-OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M(-4,0)是x轴上的一个点,点P是坐标平面内一点.若A、B、M、P四点能构成平行四边形,请写出满足条件的所有点P的坐标(不要解题过程).

▼优质解答
答案和解析
(1)设直线AB的解析式为:y=kx+b(k≠0).
∵点A(-4,4),点B(0,2)在直线AB上,
∴
,解得
,
∴直线AB的解析式为:y=-
x+2;
(2)不变.
理由如下:
过点A分别作x轴、y轴的垂线,垂足分别为E、F,如图1.
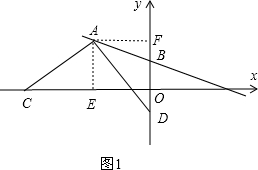
则∠AEC=∠AFD=90°,
又∵∠BOC=90°,
∴∠AEF=90°,
∴∠DAE+∠DAF=90°,
∵∠CAD=90°,
∴∠DAE+∠CAE=90°,
∴∠CAE=∠DAF.
∵A(-4,4),
∴OE=AF=AE=OF=4.
在△AEC和△AFD中
∴△AEC≌△AFD(ASA),
∴EC=FD.
∴OC-OD=(OE+EC)-(FD-OF)=OE+OF=8.
故OC-OD的值不发生变化,值为8;
(3)∵A(-4,4),B(0,2),M(-4,0),
∴AM=4,BM=
=2
,AB=
=2
,
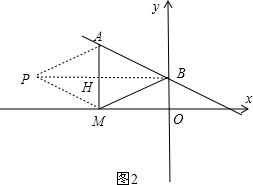
①当AM为对角线时,连接BP交AM于点H,连接PA、PM,如图2,
�
(1)设直线AB的解析式为:y=kx+b(k≠0).
∵点A(-4,4),点B(0,2)在直线AB上,
∴
|
|
∴直线AB的解析式为:y=-
| 1 |
| 2 |
(2)不变.
理由如下:
过点A分别作x轴、y轴的垂线,垂足分别为E、F,如图1.

则∠AEC=∠AFD=90°,
又∵∠BOC=90°,
∴∠AEF=90°,
∴∠DAE+∠DAF=90°,
∵∠CAD=90°,
∴∠DAE+∠CAE=90°,
∴∠CAE=∠DAF.
∵A(-4,4),
∴OE=AF=AE=OF=4.
在△AEC和△AFD中
|
∴△AEC≌△AFD(ASA),
∴EC=FD.
∴OC-OD=(OE+EC)-(FD-OF)=OE+OF=8.
故OC-OD的值不发生变化,值为8;
(3)∵A(-4,4),B(0,2),M(-4,0),
∴AM=4,BM=
| 42+22 |
| 5 |
| (-4)2+(4-2)2 |
| 5 |
①当AM为对角线时,连接BP交AM于点H,连接PA、PM,如图2,

�
看了 如图1,在平面直角坐标系中,...的网友还看了以下:
如图,抛物线y=ax2+bx-3经过点A(2,-3),与x轴负半轴交于点B,与y轴交于点C,且OC 2020-06-12 …
在平面直角坐标系中直线y=x+1和y=-¾x+3交于点A,直线y=x+1交x轴于点B,直线y=-¾ 2020-06-14 …
如图,在平面直角坐标系xOy中,直线y=−43x+8与x轴,y轴分别交于点A,点B,点D在y轴的负 2020-06-14 …
一次函数y=1/3+1的图像与x轴,y轴分别交与A,B,点C的坐标为(2,0)(1)求直线BC的函 2020-06-14 …
如图,函数y=x-3的图象分别交x轴、y轴于点A、B,点C坐标为(-1,0).一条抛物线经过A、B 2020-07-20 …
抛物线y=ax2+bx(a≠0)经过点A(1,94),对称轴是直线x=2,顶点是D,与x轴正半轴的 2020-07-21 …
已知圆C:,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A、B两点,点P(-3,0)(1)若 2020-07-30 …
高2数学,关于圆的.帮帮忙已知圆C:(x4)^2y^2=4,圆D的圆心D在Y轴上且与圆C外切,圆D 2020-07-31 …
过点a(3,1)的直线与x轴的夹角为135度与y轴的正半轴交与点b直线ac交y轴与点c点c在点b方 2020-08-02 …
已知二次函数y=x2-2mx+m2-4的图象与x轴交于A、B两点(点A在点B的左边),且与y轴交于 2020-08-03 …