早教吧作业答案频道 -->数学-->
如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF(1)求证:AF=CF;(2)若∠BAF=35°,求∠BFC的度数.
题目详情
如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF
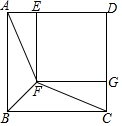
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.
▼优质解答
答案和解析
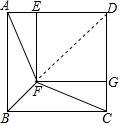 (1)证明:∵四边形ABCD和四边形DEFG都是正方形,
(1)证明:∵四边形ABCD和四边形DEFG都是正方形,
∴AD=CD,ED=GD,FE=FG.
∴AD-ED=CD-GD.
∴AE=CG.
在△AFE和△CFG中
,
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2) 由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
连接DF,
∵四边形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°-∠CFG-∠GFD=180°-35°-45°=100°.
即∠BFC=100°.
 (1)证明:∵四边形ABCD和四边形DEFG都是正方形,
(1)证明:∵四边形ABCD和四边形DEFG都是正方形,∴AD=CD,ED=GD,FE=FG.
∴AD-ED=CD-GD.
∴AE=CG.
在△AFE和△CFG中
|
∴△AFE≌△CFG(SAS),
∴AF=CF;
(2) 由(1)得△AEF≌△CGF,
∴∠AFE=∠CFG.
又∵AB∥EF,∠BAF=35°,
∴∠AFE=∠CFG=∠BAF=35°.
连接DF,
∵四边形DEFG是正方形,
∴∠DFG=45°.
∴∠BFC=180°-∠CFG-∠GFD=180°-35°-45°=100°.
即∠BFC=100°.
看了 如图,四边形ABCD和四边形...的网友还看了以下:
RT三角形ABC中,∠c=90度,点D在边BC上,BD=2CD,把三角形ABC绕着点D逆时针旋转a 2020-04-06 …
1一个多边形有35条对角线,这个多边形的边数是?P102四边形ABCD中,∠A=90°∠B:∠D= 2020-04-27 …
1.(1)三角形ABC中,BD平分角ABC,CD平分三角形ABC的外角角ACE,BD,CD交于点D 2020-05-16 …
等高线地形图表示的是()A.同一海拔高度的地形等高线地形图表示的是()A.同一海拔高度的地形B.地 2020-05-17 …
1.是否存在一个多边形,它的每个外交都等于相邻内角的1/4?为什么?2.在四边形ABCD中,∠a+ 2020-05-21 …
英语中的'd的完整形式'd的完整形式有哪些?是had,should吗? 2020-05-21 …
在Rt三角形ACB中,角C=90度,角A=30度,点D(与点A不重合)在边AC上,且AD小于CD, 2020-06-02 …
四边形ABED是一个直角梯形,角D为90度,其中AB=2厘米,AD=5厘米,DE=10厘米.如果三 2020-06-04 …
个直立的火柴盒在桌面倒下,启迪人们发现了勾股定理的一种新的验证方法,如图,火柴盒的一个侧面ABCD 2020-06-10 …
1.在等边三角形ABC中,向量AB与向量BC的夹角为A.90度B.60度C.120度D.45度(为 2020-06-12 …