早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,点A在X轴正半轴上,B在Y轴的负半轴,过点B画MN∥x轴;C是Y轴上一点,连接AC,作CD⊥CA.(1)如图(1),请直接写出∠CA0与∠CDB的数量关系.(2)如图(2),
题目详情
如图,在平面直角坐标系中,点A在X轴正半轴上,B在Y轴的负半轴,过点B画MN∥x轴;C是Y轴上一点,连接AC,作CD⊥CA.
(1)如图(1),请直接写出∠CA0与∠CDB的数量关系.
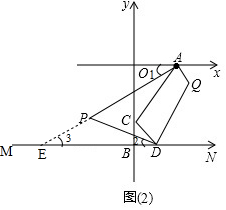
(2)如图(2),在题(1)的条件下,∠CAO的角平分线与∠CDB的角平分线相交于点P,求∠APD的度数.
(3)如图(2),在题(1)、(2)的条件下,∠CAX的角平分线与∠CDN的角平分线相交于点Q,请直接写出∠APD与∠AQD数量关系.
(4)如图(3),点C在Y轴的正半轴上运动时,∠CAO的角平分线所在的直线与∠CDB的角平分线相交于点P,∠APD的大小是否变化?若不变,直接写出其值;若变化,说明理由.
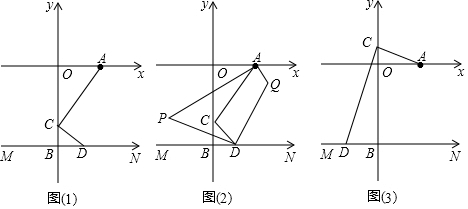
(1)如图(1),请直接写出∠CA0与∠CDB的数量关系.
(2)如图(2),在题(1)的条件下,∠CAO的角平分线与∠CDB的角平分线相交于点P,求∠APD的度数.
(3)如图(2),在题(1)、(2)的条件下,∠CAX的角平分线与∠CDN的角平分线相交于点Q,请直接写出∠APD与∠AQD数量关系.
(4)如图(3),点C在Y轴的正半轴上运动时,∠CAO的角平分线所在的直线与∠CDB的角平分线相交于点P,∠APD的大小是否变化?若不变,直接写出其值;若变化,说明理由.

▼优质解答
答案和解析
(1)如图,∵CD⊥CA,
∴∠ACO+∠DCB=90°,
∵∠AOC=90°,
∴∠ACO+∠OAC=90°,
∴∠DCB=∠OAC,
又∵∠CBD=90°,
∴∠DCB+∠CDB=90°,
∴∠CAO+∠CDB=90°;
(2)如图2,延长AP交MN于点E,
∵AP平分∠CAO、DP平分∠CDB,
∴∠1=
∠CAO、∠2=
∠CDB,
∵∠CAO+∠CDB=90°,
∴∠1+∠2=45°,
∵MN∥OA,
∴∠1=∠3,
∴∠APD=∠2+∠3=∠1+∠3=45°;
(3)∵AP平分∠OAC、AQ平分∠CAx,
∴∠PAC=
∠OAC、∠QAC=
∠CAx,
∵∠OAC+∠CAx=180°,
∴∠PAQ=∠PAC+∠CAQ=
(∠OAC+∠CAx)=90°,
同理得∠PDQ=90°,
∴∠APD+∠AQD=360°-(∠PAQ+∠PDQ)=180°;
(4)∠APD的大小不变,为45°;
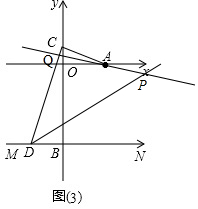
设∠CAQ=2α,∠CQA=2β,
∵∠ACD=90°,
∴∠CAQ+∠CQA=90°,即2α+2β=90,α+β=45,
∵AO∥MN,
∴∠CQA=∠CDB=2β,
∵AQ平分∠CAQ、DB平分∠CDB,
∴∠QDP=
∠CDB=β,∠CAQ=
∠CAQ=α,
则∠CQA=90°-∠CAQ=90°-α,
∴∠APD=∠CQA-∠CDB=90°-α-β=45°.
∴∠ACO+∠DCB=90°,
∵∠AOC=90°,
∴∠ACO+∠OAC=90°,
∴∠DCB=∠OAC,
又∵∠CBD=90°,
∴∠DCB+∠CDB=90°,
∴∠CAO+∠CDB=90°;
(2)如图2,延长AP交MN于点E,

∵AP平分∠CAO、DP平分∠CDB,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠CAO+∠CDB=90°,
∴∠1+∠2=45°,
∵MN∥OA,
∴∠1=∠3,
∴∠APD=∠2+∠3=∠1+∠3=45°;
(3)∵AP平分∠OAC、AQ平分∠CAx,
∴∠PAC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OAC+∠CAx=180°,
∴∠PAQ=∠PAC+∠CAQ=
| 1 |
| 2 |
同理得∠PDQ=90°,
∴∠APD+∠AQD=360°-(∠PAQ+∠PDQ)=180°;
(4)∠APD的大小不变,为45°;

设∠CAQ=2α,∠CQA=2β,
∵∠ACD=90°,
∴∠CAQ+∠CQA=90°,即2α+2β=90,α+β=45,
∵AO∥MN,
∴∠CQA=∠CDB=2β,
∵AQ平分∠CAQ、DB平分∠CDB,
∴∠QDP=
| 1 |
| 2 |
| 1 |
| 2 |
则∠CQA=90°-∠CAQ=90°-α,
∴∠APD=∠CQA-∠CDB=90°-α-β=45°.
看了 如图,在平面直角坐标系中,点...的网友还看了以下:
(1)x/a+x/b-a+a/a+b(a不等于0,axa不等于bxb)(2)(mx-n)(m+n) 2020-04-07 …
已知a,b,c成等比数列,如果a,x,b和b,y,c都成等差数列,则a/x + c/y=?下面是某 2020-05-16 …
已知二次函数f(x)=x^2+x1.若方程f(a^x)-a^(x+1)=5(a>0,a不等于1)在 2020-05-19 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
x^3+a*x+b=0(modp)其中p为任意素数,a,b为任意整数.求在modp意义下的正整数x 2020-07-22 …
下列关于x的方程是分式方程的是B.x-1/7+a=3-xC.x/a-a/b=b/a-x/b因为我可 2020-07-30 …
因式分解初一!50分哦!(1)由(x+a)(x+b)=x^2+(a+b)x+ab,可得x^2+(a+ 2020-10-31 …
有两条式子:若x1,x2是一元二次方程ax的平方+bx+c=0(a不等于0)的两根,则x1+x2=- 2020-11-07 …
1.已知集合A={x│x≤-1,或x≥2},B={x│4x+p>0},且满足B真包含于A,则实数P的 2020-11-19 …
1.已知集合A={x|x^2-3x+2=0},B={x|ax^2+2ax-5=0},求实数a的取值范 2020-12-01 …