早教吧 育儿知识 作业答案 考试题库 百科 知识分享
早教吧作业答案频道 -->数学-->

为了解甲、乙两个教学班级（每班学生数均为50人）的教学效果，期末考试后，对甲、乙两个班级的学生成绩进行统计分析，画如图甲班学生布线频率分布直方图和乙班学生成绩频数分布表

题目详情
为了解甲、乙两个教学班级（每班学生数均为50人）的教学效果，期末考试后，对甲、乙两个班级的学生成绩进行统计分析，画如图甲班学生布线频率分布直方图和乙班学生成绩频数分布表，记成绩不低于80分为优秀．
作业帮
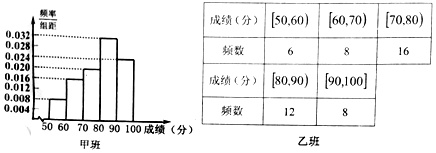
（1）根据频率分布直方图及频数分布表，填写下面2×2列联表，并判断有多大的把握认为：“成绩优秀”与所在教学班级有关．
甲班 乙班 总计
成绩优秀 ___   ___ ___  
成绩不优秀 ___ ___ ___
总计 ___ ___ ___
附：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥k） 0.25 0.15 0.10 0.05 0.025
k 1.322 2.072 2.706 3.840 5.024
（2）在甲、乙两个班成绩不及格（低于60分）的学生中任选两人，记其中甲班的学生人数为ξ，求ξ的概率分布列与数学期望．为了解甲、乙两个教学班级（每班学生数均为50人）的教学效果，期末考试后，对甲、乙两个班级的学生成绩进行统计分析，画如图甲班学生布线频率分布直方图和乙班学生成绩频数分布表，记成绩不低于80分为优秀．
作业帮
（1）根据频率分布直方图及频数分布表，填写下面2×2列联表，并判断有多大的把握认为：“成绩优秀”与所在教学班级有关．
甲班 乙班 总计
成绩优秀 ___   ___ ___  
成绩不优秀 ___ ___ ___
总计 ___ ___ ___
附：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥k） 0.25 0.15 0.10 0.05 0.025
k 1.322 2.072 2.706 3.840 5.024
（2）在甲、乙两个班成绩不及格（低于60分）的学生中任选两人，记其中甲班的学生人数为ξ，求ξ的概率分布列与数学期望．
作业帮

甲班 乙班 总计
成绩优秀 ___   ___ ___  
成绩不优秀 ___ ___ ___
总计 ___ ___ ___
甲班 乙班 总计 成绩优秀 ___   ___ ___   成绩不优秀 ___ ___ ___ 总计 ___ ___ ___ 甲班 乙班 总计 甲班乙班总计 成绩优秀 ___   ___ ___   成绩优秀 ___   ___ ___   成绩不优秀 ___ ___ ___ 成绩不优秀 ___ ___ ___ 总计 ___ ___ ___ 总计 ___ ___ ___2
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥k） 0.25 0.15 0.10 0.05 0.025
k 1.322 2.072 2.706 3.840 5.024
（2）在甲、乙两个班成绩不及格（低于60分）的学生中任选两人，记其中甲班的学生人数为ξ，求ξ的概率分布列与数学期望．
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
n(ad-bc)2 (a+b)(c+d)(a+c)(b+d) n(ad-bc)2 n(ad-bc)2)2)22 (a+b)(c+d)(a+c)(b+d) (a+b)(c+d)(a+c)(b+d)
P（K2≥k） 0.25 0.15 0.10 0.05 0.025
k 1.322 2.072 2.706 3.840 5.024
P（K2≥k） 0.25 0.15 0.10 0.05 0.025 k 1.322 2.072 2.706 3.840 5.024 P（K2≥k） 0.25 0.15 0.10 0.05 0.025 P（K2≥k）20.250.150.100.050.025 k 1.322 2.072 2.706 3.840 5.024 k1.3222.0722.7063.8405.024
▼优质解答
答案和解析
（Ⅰ）根据频率分布直方图可得甲班的成绩“优秀”的人数，（0.032+0.024）×10×50=28，
“不优秀”的人数：50-28=22．
根据已知表格可得：乙班的成绩“优秀”的人数，12+8=20，
“不优秀”的人数：50-20=30．
可得以下表格：
甲班乙班总计
成绩优秀282048
成绩不优秀223052
总计5050100
甲班乙班总计成绩优秀282048成绩不优秀223052总计5050100甲班乙班总计甲班甲班乙班乙班总计总计成绩优秀282048成绩优秀成绩优秀282820204848成绩不优秀223052成绩不优秀成绩不优秀222230305252总计5050100总计总计50505050100100根据列联表数据，K2=
100(28×30-22×20)2
48×52×50×50
≈2.564>2.072．…（5分）
所以，有85%的把握认为“成绩优秀”与所在教学班级有关．…（6分）
（Ⅱ）由已知甲、乙两班级不及格人数分别是：4人、6人ξ的所有取值为：0，1，2…（7分）P(ξ=0)=
C
2
6
C
2
10
=
1
3
，P(ξ=1)=
C
1
6
C
1
4
C
2
10
=
8
15
，P(ξ=2)=
C
2
4
C
2
10
=
2
15

ξ012
P
1
3
8
15
2
15
…（10分）
所求分布列的数学期望为：Eξ=0×
1
3
+1×
8
15
+2×
2
15
=
4
5
…（12分） K2=
100(28×30-22×20)2
48×52×50×50
≈2.564>2.072．…（5分）
所以，有85%的把握认为“成绩优秀”与所在教学班级有关．…（6分）
（Ⅱ）由已知甲、乙两班级不及格人数分别是：4人、6人ξ的所有取值为：0，1，2…（7分）P(ξ=0)=
C
2
6
C
2
10
=
1
3
，P(ξ=1)=
C
1
6
C
1
4
C
2
10
=
8
15
，P(ξ=2)=
C
2
4
C
2
10
=
2
15

ξ012
P
1
3
8
15
2
15
…（10分）
所求分布列的数学期望为：Eξ=0×
1
3
+1×
8
15
+2×
2
15
=
4
5
…（12分） 2=
100(28×30-22×20)2
48×52×50×50
100(28×30-22×20)248×52×50×50100(28×30-22×20)2100(28×30-22×20)2100(28×30-22×20)2248×52×50×5048×52×50×5048×52×50×50≈2.564>2.072．…（5分）
所以，有85%的把握认为“成绩优秀”与所在教学班级有关．…（6分）
（Ⅱ）由已知甲、乙两班级不及格人数分别是：4人、6人ξ的所有取值为：0，1，2…（7分）P(ξ=0)=
C
2
6
C
2
10
=
1
3
，P(ξ=1)=
C
1
6
C
1
4
C
2
10
=
8
15
，P(ξ=2)=
C
2
4
C
2
10
=
2
15

ξ012
P
1
3
8
15
2
15
…（10分）
所求分布列的数学期望为：Eξ=0×
1
3
+1×
8
15
+2×
2
15
=
4
5
…（12分） P(ξ=0)=
C
2
6
C
2
10
C
2
6
C
2
10
C
2
6
C
2
6
C
2
6
C
2
6
C
2
6
CC
2
6
2
2
6
6
C
2
10
C
2
10
C
2
10
C
2
10
C
2
10
CC
2
10
2
2
10
10=
1
3
13111333，P(ξ=1)=
C
1
6
C
1
4
C
2
10
=
8
15
，P(ξ=2)=
C
2
4
C
2
10
=
2
15

ξ012
P
1
3
8
15
2
15
…（10分）
所求分布列的数学期望为：Eξ=0×
1
3
+1×
8
15
+2×
2
15
=
4
5
…（12分） P(ξ=1)=
C
1
6
C
1
4
C
2
10
C
1
6
C
1
4
C
2
10
C
1
6
C
1
4
C
1
6
C
1
4
C
1
6
C
1
6
C
1
6
CC
1
6
1
1
6
6
C
1
4
C
1
4
C
1
4
CC
1
4
1
1
4
4
C
2
10
C
2
10
C
2
10
C
2
10
C
2
10
CC
2
10
2
2
10
10=
8
15
815888151515，P(ξ=2)=
C
2
4
C
2
10
=
2
15

ξ012
P
1
3
8
15
2
15
…（10分）
所求分布列的数学期望为：Eξ=0×
1
3
+1×
8
15
+2×
2
15
=
4
5
…（12分） P(ξ=2)=
C
2
4
C
2
10
C
2
4
C
2
10
C
2
4
C
2
4
C
2
4
C
2
4
C
2
4
CC
2
4
2
2
4
4
C
2
10
C
2
10
C
2
10
C
2
10
C
2
10
CC
2
10
2
2
10
10=
2
15
215222151515
ξ012
P
1
3
8
15
2
15
ξ012P
1
3
8
15
2
15
ξ012ξξ001122P
1
3
8
15
2
15
PP
1
3
1
3
1
3
13111333
8
15
8
15
8
15
815888151515
2
15
2
15
2
15
215222151515…（10分）
所求分布列的数学期望为：Eξ=0×
1
3
+1×
8
15
+2×
2
15
=
4
5
…（12分） Eξ=0×
1
3
13111333+1×
8
15
815888151515+2×
2
15
215222151515=
4
5
45444555…（12分）
看了 为了解甲、乙两个教学班级（每...的网友还看了以下：

已知甲乙两数的和是231，已知甲数的末位是0，如果把甲数末位的0去掉，正好等于乙数，那么，甲数是， 　2020-04-27 …

甲.乙两个数的和是252.已知甲数末是0,把甲数末位0去掉,正好乙数的一半,甲数是多少? 　2020-04-27 …

甲乙两数的和是252.已知甲数的末位是0如果把甲数末尾的0去掉,正好是乙数的一半.甲数是多少 　2020-04-27 …

甲乙两数和是252,已知甲数的末位是0,如果把甲数末位的0去掉,正好是乙数的一半,甲数是多少? 　2020-04-27 …

甲、乙两组学生周末骑车春游，出发点到目的地的距离是5千米，他们同时出发且甲组同学中途休息10分钟， 　2020-04-27 …

甲、乙两数的和是378.已知甲数的末尾数是0,如果把甲数末尾的0去掉,正好是乙数的2倍,甲数是多少 　2020-06-14 …

甲、乙两数的和是378,已知甲数末位是0,如果把甲数末位的0去掉,正好是乙数的2倍,甲数是多少? 　2020-06-14 …

某班级45名学生在期末学情分析考试中，分数段在120～130分的频率为0.2，则该班级在这个分数段内 　2020-12-06 …

爱因斯坦提出：“人的差异在于业余时间”．某校要对本校高二年级900名学生的周末学习时间进行调查．现从 　2020-12-06 …

爱因斯坦提出：“人的差异在于业余时间”．某校要对本校高一学生的周末学习时间进行调查．现从中抽取50个 　2020-12-16 …

©2023 zaojiaoba.cn 手机版 | 关于早教吧