如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点），则下列结论：①当x＞3时，y＜0；②3a+b＞0；③

Question

如图，抛物线y=ax 2 +bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点），则下列结论： ① 当x＞3时，y＜0； ② 3a +b＞0； ③ ﹣1≤a≤﹣ 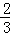； ④ 3≤n≤4中，正确的是（　　） 。

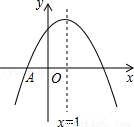
A ． ①② B ． ③④ C ． ①④ D ． ①③

 

Answer 1

D.

分 析：
①∵抛物线y=ax2+bx+c与x轴交于点A（-1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x=-∴b=-2a，∴3a+b=3a-2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（-1，0），（3，0），∴-1×3=-3，∴，则a=-．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴-1≤-≤-，即-1≤a≤-．故③正确；④根据题意知，a=-，-=1，∴b=-2a=，∴n=a+b+c=∵2≤c≤3，∴≤≤4，即≤n≤4．故④错误．综上所述，正确的说法有①③．故选D．
考点：
二次函数图象与系数的关系．