早教吧作业答案频道 -->数学-->
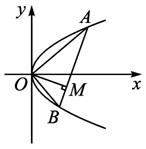
如图,设点A和B是抛物线y2=4px上原点以外的两个动点,已知OA⊥OB,OM⊥AB,求动点M的轨迹方程,并说明它表示什么曲线.
题目详情
如图,设点A和B是抛物线y 2 =4px上原点以外的两个动点,已知OA⊥OB,OM⊥AB,求动点M的轨迹方程,并说明它表示什么曲线.
▼优质解答
答案和解析
点A、B在抛物线y2=4px上,设A( yA) B( yB) 则=( yA) =( yB) =( yB-yA). 因为⊥,所以·+yA·yB=0,即yA·yB=-16p2. 设M=(x y),则=(x y) =(-x yA-y) =(-x yB-y). 因为⊥,所以x·+y(yB-yA)=0 即x·+y=0. 又因为A、B、M三点共线,所以∥ 即(-x)(yB-y)=(-x)(yA-y). 化简得yA+yB= 所以x·+y=0, 即x2+y2-4px=0. 因为A、B是原点以外的两点,所以x≠0.所以点M的轨迹是以(2p 0)为圆心,以2p为半径的圆(去掉原点).
看了 如图,设点A和B是抛物线y2...的网友还看了以下:
已知二次函数Y=F[X]的图像是开口向上的抛物线,F[-5]、F[-1]、F[4]、F[7]这四个函 2020-03-30 …
如图,已知二次函数y=x^2+bx+c的图象过a(1,0),c(0,-3),(1)求此抛物线的解析 2020-04-26 …
(2013•普陀区二模)如图,抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A、B, 2020-05-13 …
如图,抛物线y=-x^2+bx+c与x轴,y轴分别相交与A(-1,0),B(0,3)两点,其顶点为 2020-05-16 …
初三数学一个二次函数的图像是以(4,-2)为顶点的抛物线,其与x轴交于A、B两点,与y轴交于C点, 2020-05-16 …
如图,已知每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,请你在图中任画一条抛物线, 2020-05-16 …
如图所示抛物线是二次函数y=ax^2+bx+c(a不等于0)的图像.则下列结论:1.abc大于如图 2020-05-16 …
聪明的人帮忙看看高一物理v-t图像的疑问如果v-t图是一开口向上的抛物线的右半部分,那么是描述什么 2020-05-21 …
如图在直角坐标系中,圆O1过点PQE三点的圆,且与X相切点E,连接PE,QE,已知道P(0,9)Q 2020-05-22 …
一个函数的图像是一条以y轴为对称轴,以原点为定点的抛物线,且经过点A(-2,2).1.求这个函数的 2020-05-23 …