早教吧作业答案频道 -->数学-->
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点(1)求证:DP∥平面ACB1.(2)求证:平面DPD1∥平面CBB1.
题目详情
直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点
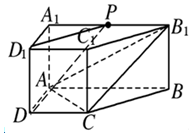
(1)求证:DP∥平面ACB1.
(2)求证:平面DPD1∥平面CBB1.

(1)求证:DP∥平面ACB1.
(2)求证:平面DPD1∥平面CBB1.
▼优质解答
答案和解析
证明:(1)∵直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,
∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点
∴CD
PB1,∴四边形DCB1P是平行四边形,∴DP∥B1C,
∵DP⊄平面ACB1,B1C⊂平面ACB1.
∴DP∥平面ACB1.
(2)由(1)知DP∥B1C,
∵直棱柱ABCD-A1B1C1D1,∴由直棱柱性质得DD1∥BB1,
∵DD1∩DP=D,B1C∩BB1=B,
DD1,DP⊂平面DD1P,B1C,BB1⊂平面CBB1,
∴平面DPD1∥平面CBB1.

∠BAD=∠ADC=90°,AB=2AD=2CD=2.P为A1B1的中点
∴CD
| ∥ |
. |
∵DP⊄平面ACB1,B1C⊂平面ACB1.
∴DP∥平面ACB1.
(2)由(1)知DP∥B1C,
∵直棱柱ABCD-A1B1C1D1,∴由直棱柱性质得DD1∥BB1,
∵DD1∩DP=D,B1C∩BB1=B,
DD1,DP⊂平面DD1P,B1C,BB1⊂平面CBB1,
∴平面DPD1∥平面CBB1.
看了 直棱柱ABCD-A1B1C1...的网友还看了以下:
1/2{1/2[1/2(1/2y-3)-3]-3}=17x-1/0.024=1-0.2x/0.08 2020-04-27 …
(1)1/1*2+1/2*3+.+1/2009*2010(2)1/2*4+1/4*6+.+1/20 2020-05-17 …
1.直接写得数1/2+1/31/2+1/41/3+1/51/4+2/31/3+3/51/6+2/7 2020-06-13 …
(1/2+1/3+1/4+...1/2013)X(1+1/2+1/3+1/4+...1/2012) 2020-07-14 …
设R^3中的一组基ξ1=(1,-2,1)T,ξ2=(0,1,1)T,ξ3=(3,2,1)T,向量α在 2020-11-02 …
初一一道数学找规律的题急用1.将1,-1/2,1/3,-1/4,1/5,-1/6,.按一定的规律排列 2020-11-03 …
正方体ABCD-A1B1C1D1棱长为1,E,F分别为棱BC,DD1上的点,如果B1E垂直于平面AB 2020-11-03 …
求一道预备班数学期中考试的答案小明在做题时发现了一个规律:1*2/1=1-2/1,2*3/1=2/1 2020-11-05 …
观察下列等式①1/√2+1=√2-1/(√2+1)(√2-1)=-1+√2②1/√3+√2=√3-√ 2020-12-07 …
高中数学抽象函数已知定义在(-1,1)上的函数f(x)满足f(1/2)=1,且对任意x,y∈(-1, 2020-12-08 …