早教吧作业答案频道 -->数学-->
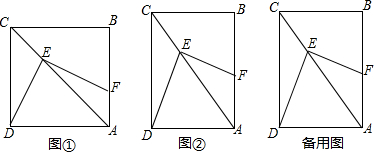
小明一直对四边形很感兴趣,在矩形ABCD中,E是AC上任意一点,连接DE,作DE⊥EF,交AB于点F.请你跟着他一起解决下列问题:(1)如图①,若AB=BC,则DE,EF有什么数量关系?请给出证明.(2
题目详情
小明一直对四边形很感兴趣,在矩形ABCD中,E是AC上任意一点,连接DE,作DE⊥EF,交AB于点F.请你跟着他一起解决下列问题:
(1)如图①,若AB=BC,则DE,EF有什么数量关系?请给出证明.
(2)如图②,若∠CAB=30°,则DE,EF又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果在矩形ABCD中,BC=mAB,那DE,EF有什么数量关系?请给出证明.
(1)如图①,若AB=BC,则DE,EF有什么数量关系?请给出证明.
(2)如图②,若∠CAB=30°,则DE,EF又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果在矩形ABCD中,BC=mAB,那DE,EF有什么数量关系?请给出证明.

▼优质解答
答案和解析
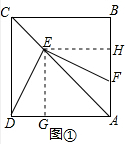 (1)DE=EF.
(1)DE=EF.
过点E作EG⊥AD与G,EH⊥AB于H,
则∠EGD=∠EHF=90°,又∠BAD=90°,
∴四边形EGAH是矩形,
∵四边形ABCD是矩形,AB=AD,
∴矩形ABCD为正方形,
∴∠EAH=45°,
∴HE=HA,
∴四边形AHEG是正方形,
∴EH=EG,∠GEH=90°,
∴∠FED-∠GEF=∠GEH-∠GEF,
即∠DEG=∠FEH,
在△EDG和△EFH中,
,
∴△EDG≌△EFH
∴DE=EF;
(2)DE=
EF.
∵∠CAB=30°,
∴
=
,
同(1)理得,∠EGD=∠EHF=90°,∠DEG=∠FEH
∴△EDG∽△EFH,
∴
=
=
,
∴DE=
EF;
(3)DE=
EF.
同(2)理得,△EDG∽△EFH,
∴
=
=
=
,
∴DE=
EF.
 (1)DE=EF.
(1)DE=EF.过点E作EG⊥AD与G,EH⊥AB于H,
则∠EGD=∠EHF=90°,又∠BAD=90°,
∴四边形EGAH是矩形,
∵四边形ABCD是矩形,AB=AD,
∴矩形ABCD为正方形,
∴∠EAH=45°,
∴HE=HA,
∴四边形AHEG是正方形,
∴EH=EG,∠GEH=90°,
∴∠FED-∠GEF=∠GEH-∠GEF,
即∠DEG=∠FEH,
在△EDG和△EFH中,
|
∴△EDG≌△EFH
∴DE=EF;
(2)DE=
| 3 |
∵∠CAB=30°,
∴
| AH |
| EH |
| 3 |
同(1)理得,∠EGD=∠EHF=90°,∠DEG=∠FEH
∴△EDG∽△EFH,
∴
| DE |
| EF |
| EG |
| EH |
| 3 |
∴DE=
| 3 |
(3)DE=
| 1 |
| m |
同(2)理得,△EDG∽△EFH,
∴
| DE |
| EF |
| EG |
| EH |
| AB |
| BC |
| 1 |
| m |
∴DE=
| 1 |
| m |
看了 小明一直对四边形很感兴趣,在...的网友还看了以下:
设函数f(x)在x=a处二阶可导,又limf'(x)/(x-a)=-1,则()A.x=a是f(x设函 2020-03-31 …
(2003•西城区模拟)Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为 2020-05-22 …
如图已知直线y=4/3x+4与x轴,y轴分别交与A,B两点,点C从O点出发沿射线OA以每秒1个单位 2020-06-04 …
如图已知直线y=4/3x+4与x轴,y轴分别交与A,B两点,点C从O点出发沿射线OA以每秒1个单位 2020-06-04 …
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出 2020-06-15 …
如图,已知直线y=43x+4与x轴、y轴分别相交于点A、B,点C从O点出发沿射线OA以每秒1个单位 2020-07-20 …
如图,在数轴上点A、B、C表示的数分别为-2、1、6,点A与点B之间的距离表示为AB,点B与点C之 2020-07-29 …
在数轴上有三个点A,B,C,回答下列问题:(1)若将点B向右移动6个单位后,三个点所表示的数最小的 2020-07-30 …
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出 2020-08-03 …
(2014•房山区一模)如图,抛物线y=-x2+bx+c经过A(-1,0)、C(0,4)两点,与x轴 2020-12-10 …