早教吧作业答案频道 -->数学-->
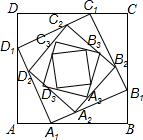
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=13a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=1
题目详情
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=
a,在边A1B1、B1C1、C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2=B1B2=C1C2=D1D2=
A1B2,….依次规律继续下去,则正方形AnBnCnDn的面积为___.
| 1 |
| 3 |
| 1 |
| 3 |

▼优质解答
答案和解析
在Rt△A1BB1中,由勾股定理可知;A1B12=A1B2+B1B2=(
a)2+(
a)2=
a2,即正方形A1B1C1D1的面积=
a2;
在Rt△A2B1B2中,由勾股定理可知:A2B22=A2B12+B2B12=(
×
a)2+(
×
a)2=(
)2a2;即正方形A2B2C2D2的面积=(
)2a2
…
∴正方形AnBnCnDn的面积=(
)na2=
a2.
故答案为:
a2.
| 2 |
| 3 |
| 1 |
| 3 |
| 5 |
| 9 |
| 5 |
| 9 |
在Rt△A2B1B2中,由勾股定理可知:A2B22=A2B12+B2B12=(
| 2 |
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 5 |
| 9 |
| 5 |
| 9 |
…
∴正方形AnBnCnDn的面积=(
| 5 |
| 9 |
| 5n |
| 9n |
故答案为:
| 5n |
| 9n |
看了 如图,正方形ABCD的边长为...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
1三角形ABC三边a b c 求证cX²-(a+b)x+c/4=0有二个不相等的实数根2三角形AB 2020-05-16 …
左下图为一阶梯截面,老鼠沿两边A-B-D的路线逃跑,猫同时沿阶梯(折线)A-C-D的路线去追,结果 2020-06-20 …
∫dx/√(x^2+a^2)最后两步:=ln|x/a+v(x^2+a^2)/a|+c1=ln|x+ 2020-07-22 …
已知等腰Rt三角形ABC的底边为AB,直线L经过直角顶点C,过点A、B分别作L的垂线AE、BF,点 2020-07-29 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
在三角形ABC中,A,B,C的对边分别为a,b,c,已知a,b,c成等比数列,cosB=3/4(1 2020-07-30 …
下列已知△ABC的两边及其中一边对角的条件中,正确的是()A.a=8,b=16,A=30°有两解B 2020-07-31 …
设三阶方阵A=(a,c1,c2)B=(b,2c1,-3c2).其中abc1c2均是三维列向量,|A| 2020-10-31 …
在三角形ABC中,a,b,c分别为角A,B,C所对的边长,且a=3,A=派/3,点D在BC边上.(一 2020-11-02 …