早教吧作业答案频道 -->数学-->
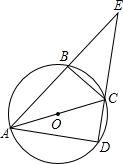
如图,AC是圆O的直径,AB、AD是圆O的弦,且AB=AD,连结BC、DC.(1)求证:△ABC≌△ADC;(2)延长AB、DC交于点E,若EC=5cm,BC=3cm,求四边形ABCD的面积.
题目详情
如图,AC是圆O的直径,AB、AD是圆O的弦,且AB=AD,连结BC、DC.
(1)求证:△ABC≌△ADC;
(2)延长AB、DC交于点E,若EC=5cm,BC=3cm,求四边形ABCD的面积.

(1)求证:△ABC≌△ADC;
(2)延长AB、DC交于点E,若EC=5cm,BC=3cm,求四边形ABCD的面积.
▼优质解答
答案和解析
(1)证明:∵AC是圆O的直径,
∴∠ABC=∠D=90°,
在Rt△ABC与Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC;
(2)由(1)知Rt△ABC≌Rt△ADC,
∴CD=BC=3,AD=AB,
∴DE=5+3=8,
∵∠EAD=∠ECB,∠D=∠EBC=90°,
∴△EAD∽△ECB,
∴
=
,
∵BE=
=4,
∴
=
,
∴AD=6,
∴四边形ABCD的面积=S△ABC+S△ACD=2×
×3×6=18cm2.
∴∠ABC=∠D=90°,
在Rt△ABC与Rt△ADC中,
|
∴Rt△ABC≌Rt△ADC;
(2)由(1)知Rt△ABC≌Rt△ADC,
∴CD=BC=3,AD=AB,
∴DE=5+3=8,
∵∠EAD=∠ECB,∠D=∠EBC=90°,
∴△EAD∽△ECB,
∴
| AD |
| BC |
| DE |
| BE |
∵BE=
| CE2-BC2 |
∴
| AD |
| 3 |
| 8 |
| 4 |
∴AD=6,
∴四边形ABCD的面积=S△ABC+S△ACD=2×
| 1 |
| 2 |
看了 如图,AC是圆O的直径,AB...的网友还看了以下:
已知圆心为C的圆经过点A(0,1)和B(-2,3),且圆心直线L:x+2y-3=0上1求圆C标准方 2020-04-27 …
1.椭圆c的焦点在x轴上,焦距为2,直线l:x-y-1=0与椭圆c交于A、B两点,F1是左焦点且F 2020-05-15 …
例求过两圆C1:X^2+Y^2-4X+2Y=0和圆C2:X^2+Y^2-2Y-4=0的交点,且圆心 2020-07-09 …
已知椭圆C的中心为坐标原点O,焦点在X轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A,B两点,向量 2020-07-24 …
圆心为C的圆经过点A(-1,1)和B(-2,-2)且圆心在直线x+y-1=0上,求,(1)圆心为C 2020-07-26 …
已知圆C的圆心坐标原点,且过点M(1,根号3)问:(1)求圆C的方程(2)已知点P是圆C上的动点, 2020-07-26 …
已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆 2020-07-31 …
已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆 2020-07-31 …
已知圆C:x^2+y^2-6x-8y+21=0,点A(1,0),O是坐标原点若以A(1,0)为圆心的 2020-10-31 …
椭球面S1是椭圆x24+y23=1绕x轴旋转而成,圆锥面S2是过点(4,0)且与椭圆x24+y23= 2020-10-31 …