早教吧作业答案频道 -->数学-->
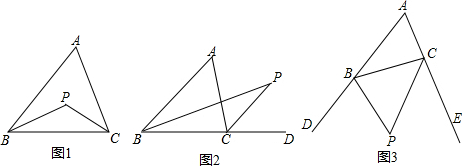
(1)如图1,点P为△ABC的内角平分线BP与CP的交点,求证:∠BPC=90°+12∠A;(2)如图2,点P为△ABC内角平分线BP与外角平分线CP的交点,请直接写出∠BPC与∠A的关系;(3)如图3,点P是△ABC的
题目详情
(1)如图1,点P为△ABC的内角平分线BP与CP的交点,求证:∠BPC=90°+
∠A;
(2)如图2,点P为△ABC内角平分线BP与外角平分线CP的交点,请直接写出∠BPC与∠A的关系;
(3)如图3,点P是△ABC的外角平分线BP与CP的交点,请直接∠BPC与∠A的关系.
| 1 |
| 2 |
(2)如图2,点P为△ABC内角平分线BP与外角平分线CP的交点,请直接写出∠BPC与∠A的关系;
(3)如图3,点P是△ABC的外角平分线BP与CP的交点,请直接∠BPC与∠A的关系.

▼优质解答
答案和解析
证明:(1)∵∠PBC+∠BCP+∠BPC=180°,
∵∠BPC=120°,
∴∠ABC+∠ACB=60°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∵∠ABC+∠ACB+∠A=180°,
∴∠BPC=90°+
∠A;
(2)∠P=
∠A,理由如下:
∵△ABC的内角平分线BP与外角平分线CP交于P,
∴∠PBC=
∠ABC,∠PCD=
∠ACD,
∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴
(∠A+∠ABC)=∠PBC+∠P=
∠ABC+∠P,
∴∠P=
∠A;
(3)∠P=90°-
∠A,理由如下:
∵BP、CP是△ABC的外角平分线,
∴∠PBC=
(∠A+∠ACB),∠PCB=
(∠A+∠ABC),
又∵∠PBC+∠PCB+∠P=180°,
∴∠P=180°-(∠PBC+∠PCB)
=180°-
(∠A+∠ACB+∠A+∠ABC)
=180°-
(180+∠A)
=90°-
∠A.
∵∠BPC=120°,
∴∠ABC+∠ACB=60°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∵∠ABC+∠ACB+∠A=180°,
∴∠BPC=90°+
| 1 |
| 2 |
(2)∠P=
| 1 |
| 2 |
∵△ABC的内角平分线BP与外角平分线CP交于P,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠P=
| 1 |
| 2 |
(3)∠P=90°-
| 1 |
| 2 |
∵BP、CP是△ABC的外角平分线,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠PBC+∠PCB+∠P=180°,
∴∠P=180°-(∠PBC+∠PCB)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
看了 (1)如图1,点P为△ABC...的网友还看了以下:
如图,∠MON=90°,点A,B分别在直线OM、ON上,BC是∠ABN的平分线.(1)如图1,若B 2020-05-17 …
以下关于中间纤维的描述不正确的是()。A.是最稳定的细胞骨架成分B.直径略小于微丝C.具有组织特异 2020-06-26 …
在三角形abc中 角c大于角b 如图1 AD垂直BC于点D AE平分角BAC(1)如图1试用含∠B 2020-06-27 …
关于皮带传动中,A是主动轮,B,C和D是从动轮.其中A带动B,B和C是同轴不同直径的轮,C带动D转 2020-07-01 …
如图所示,直线EF‖GH,A是直线EF上一点,B,C,D分别是直线GH上的三点,且AB=AC,D 2020-07-09 …
问题:已知一组平行直线a∥b∥c,求作等边三角形ABC,使点A、B、C分别在直线a,b,c上.小明同 2020-11-02 …
足球比赛的计分规则为:胜一场得2分,负一场得1分A如果胜6场,总积分为15分B如果总积分为16分,则 2020-12-26 …
如图a,一条笔直的公路上有A,B,C三地,B,C两地相距150千米,甲、乙两辆汽车分别……如图a,一 2020-12-27 …
如图所示,直线y=-4/3x+4与y轴和x轴分别交于点A,点D,与直线y...如图所示,直线y=-4 2021-01-10 …
已知如图,直线AB:y=-x+8与x轴,y轴分别交与点B,A,过点B作直线AB的垂线交y轴与点D已知 2021-01-11 …