阅读甲、乙两图，回答有关问题(1)从水能蕴藏量、航运价值两方面比较R1、R两条河流的差异．并解释其原因。(2)分析A、B两港口相同的区位条

Question

阅读甲、乙两图，回答有关问题

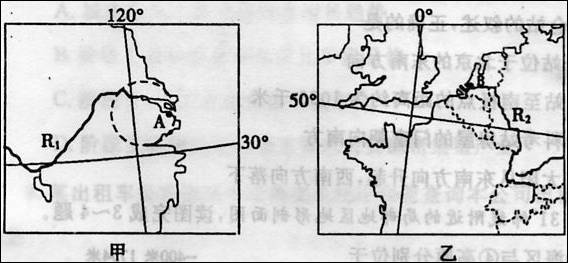
(1) 从水能蕴藏量、航运价值两方面比较 R1 、 R 两条河流的差异．并解释其原因。

(2) 分析 A 、 B 两港口相同的区位条件。

(3) 一艘满载纺织品的货轮从 A 港驶向 B 港，于某日北京时间 12 点途经斯里兰卡附近海域时，发现一艘失事油轮泄露的大量原油在海面迅速扩散．油膜漂移方向与货轮航行方向一致。请判断此时货轮桅杆影子的朝向。并简要说明理由．

(4) 近年来，甲图中圆圈所示地区受到本国乃至世界的关注，成为国内外投资者关注的“热土”。试分析该地区吸引投资者有利的社会经济条件．

Answer 1

(1) ①河的水能资源比②河丰富，因为①河流经地区落差大，②河主要流经平原地区；②河的航运价值比①河大，因为⑦河流量、流速较①河平稳，且⑦河流经地区经济发达，运输量变大。

(2) 既位于大洋沿岸，又位于大河河口，水域 ( 航行，停泊 ) 条件好；沿岸地形平坦开阔，筑港条件优越；经济腹地辽阔，且经济发达。

  (3) 西北    货轮从 A 港驶向 B 港，在斯里兰卡附近海域自东向西航行，由于油膜漂移方向与货轮航行方向一致，可知北印度洋洋流自东向西流，此时北半球为冬季，桅杆影子应位于偏北方向；当北京时问 12 点时，太阳直射 120 。 E ，位于 120 。 E 西侧的斯里兰卡影子应位于偏西方向。

  (4) 交通与基础设施完善，海陆空交通便利；科技和文化教育事业发达；市场广阔；雄厚

的经济基础；劳动力丰富；国家的优惠政策