早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在P上.(1)求圆的半径及圆心P的坐标;(2)M为劣弧OB的中点,求证:AM是∠OAB的平分线;(3)连接BM并延长交y轴于点N
题目详情
如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在 P上.
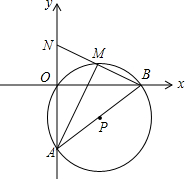
(1)求圆的半径及圆心P的坐标;
(2)M为劣弧
的中点,求证:AM是∠OAB的平分线;
(3)连接BM并延长交y轴于点N,求N,M点的坐标.

(1)求圆的半径及圆心P的坐标;
(2)M为劣弧
 |
| OB |
(3)连接BM并延长交y轴于点N,求N,M点的坐标.
▼优质解答
答案和解析
(1)∵O(0,0),A(0,-6),B(8,0),
∴OA=6,OB=8,
∴AB=
=10,
∵∠AOB=90°,
∴AB为 P的直径,
∴ P的半径是5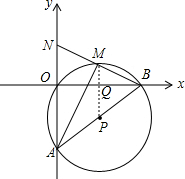
∵点P为AB的中点,
∴P(4,-3);
(2)∵M点是劣弧OB的中点,
∴
=
,
∴∠OAM=∠MAB,
∴AM为∠OAB的平分线;
(3)连接PM交OB于点Q,如图,
∵
=
,
∴PM⊥OB,BQ=OQ=
OB=4,
在Rt△PBQ中,PQ=
=
=3,
∴MQ=2,
∴M点的坐标为(4,2);
∵MQ∥ON,
而OQ=BQ,
∴MQ为△BON的中位线,
∴ON=2MQ=4,
∴N点的坐标为(0,4).
∴OA=6,OB=8,
∴AB=
| 62+82 |
∵∠AOB=90°,
∴AB为 P的直径,
∴ P的半径是5

∵点P为AB的中点,
∴P(4,-3);
(2)∵M点是劣弧OB的中点,
∴
 |
| OM |
 |
| BM |
∴∠OAM=∠MAB,
∴AM为∠OAB的平分线;
(3)连接PM交OB于点Q,如图,
∵
 |
| OM |
 |
| BM |
∴PM⊥OB,BQ=OQ=
| 1 |
| 2 |
在Rt△PBQ中,PQ=
| PB2-BQ2 |
| 52-42 |
∴MQ=2,
∴M点的坐标为(4,2);
∵MQ∥ON,
而OQ=BQ,
∴MQ为△BON的中位线,
∴ON=2MQ=4,
∴N点的坐标为(0,4).
看了 如图,在平面直角坐标系中,O...的网友还看了以下:
计数原理有五张卡片,他们的正反面分别写有0与1,2与3,4与5,6与7,8与9,将其中任意三张排放 2020-04-09 …
直线的斜率若三点A(1,4),B(2,m),C(m,2)是△ABC的三个顶点,求实数m的取值范围. 2020-04-27 …
“m=-2”是“直线(m+2)x+3my+1=0与(m-2)x+(m+2)y-3=0垂直的什么条件 2020-04-27 …
若二次三项式9x^2-(m-6)+m-2是一个完全平方式,求m的值 2020-05-13 …
已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为()A.-2B.2C.±2D.0 2020-05-13 …
“m>2”是“方程x^2/(m-2) +y^2/(5-m) =1表示的曲线是椭圆”的()?A 充分 2020-05-16 …
已知m属于R,mx-(m2+1)y=4m斜率取值范围解答已经看过了,就是不明白m-1/m≥2√(m 2020-06-04 …
求证:对于任意实数m,点M(m,-m^2)都不在二次函数y+-1/2(x+1)^2+2上-m^2是 2020-06-12 …
已知圆C:(x-m)^2+(y-根号3m)^2=m^2)是否存在直线L,使得对于任意的实数m,都有 2020-06-12 …
若m=p/q,其中p与q为非零整数,要使m是一个整数,则必须满足下面哪个条件(1)m^2是一个整数 2020-06-20 …