如图，已知双曲线C：x2a2-y2b2=1（a>0，b>0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q，若∠PAQ=60°，且

Question

如图，已知双曲线C： (x2)/(a2)- (y2)/(b2)=1（a>0，b>0）的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P，Q，若∠PAQ=60°，且

OQ

=3

OP

，则双曲线的离心率为___．

Answer 1

因为∠PAQ=60°且

OQ

=3

OP

，
所以△QAP为等边三角形，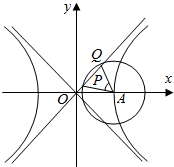
设AQ=2R，则OP=R，
渐近线方程为y=(b)/(a)x，A（a，0），取PQ的中点M，则AM=(|-ab|)/(√(a2+b2))
由勾股定理可得（2R）²-R²=（(|-ab|)/(√(a2+b2))）²，
所以（ab）²=3R²（a²+b²）①
在△OQA中，((3R)2+(2R)2-a2)/(2×3R×2R)=(1)/(2)，所以7R²=a²②
①②结合c²=a²+b²，可得e=(c)/(a)=(√(7))/(2)．
故答案为：(√(7))/(2)