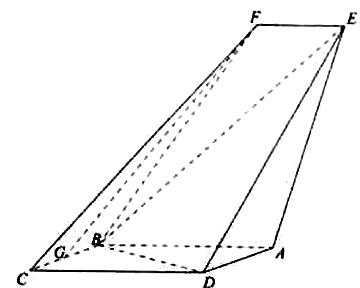
如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF||AB，AB=2，BC=EF=1，AE=，DE=3，∠BAD=60º，G为BC的中点.(Ⅰ)求证：FG||平面BED；(Ⅱ)求证：平面BED⊥平面AED；(Ⅲ)求直线EF与平面BED

Question

如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF||AB，AB=2，BC=EF=1，AE=，DE=3，∠BAD=60º，G为BC的中点.

(Ⅰ)求证：FG||平面BED；

(Ⅱ)求证：平面BED⊥平面AED；

(Ⅲ)求直线EF与平面BED所成角的正弦值.

Answer 1

（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）

（Ⅱ）证明：在中，，由余弦定理可，进而可得，即，又因为平面平面平面；平面平面，所以平面.又因为平面，所以平面平面.

（Ⅲ）因为，所以直线与平面所成角即为直线与平面所成角.过点作于点，连接，又因为平面平面，由（Ⅱ）知平面，所以直线与平面所成角即为.在中，，由余弦定理可得，所以，因此，在中，，所以直线与平面所成角的正弦值为.

考点：直线与平面平行和垂直、平面与平面垂直、直线与平面所成角