早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,直线AB交两坐标轴于A、B两点,OA>OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根.(1)求cos∠ABO的值;(2)以线段AB的长为边作正方形ABCD(如图所示),
题目详情
如图,在平面直角坐标系中,直线AB交两坐标轴于A、B两点,OA>OB,且OA、OB的长分别是一元二次方程x2-7x+12=0的两根.
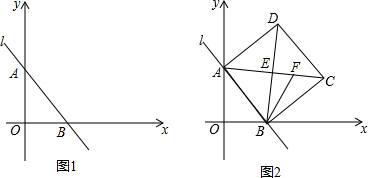
(1)求cos∠ABO的值;
(2)以线段AB的长为边作正方形ABCD(如图所示),对角线AC、BD交于点E,∠CBD的平分线BF交AC于F,求CF的长;
(3)若点M是y轴上任一点,点N是坐标平面内一点,若以A、B、M、N为顶点的四边形是菱形,请直接写出N点的坐标.

(1)求cos∠ABO的值;
(2)以线段AB的长为边作正方形ABCD(如图所示),对角线AC、BD交于点E,∠CBD的平分线BF交AC于F,求CF的长;
(3)若点M是y轴上任一点,点N是坐标平面内一点,若以A、B、M、N为顶点的四边形是菱形,请直接写出N点的坐标.
▼优质解答
答案和解析
(1)解一元二次方程x2-7x+12=0得,
x1=3,x2=4,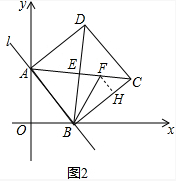
∵OA>OB,
∴OA=4,OB=3,
由勾股定理得,AB=
=5,
∴cos∠ABO=
=
;
(2)如图2,过F作FH⊥BC于H,
∵BF是∠CBD的平分线,
∴EF=HF,
又∵四边形ABCD为正方形,
∴EF=HF=CH,又∵AB=5,
∴CE=5sin45°=
,
设CF=x,则EF=HF=CH=
-x,
由勾股定理得,CF2=FH2+HC2,即x2=2(
-x)2,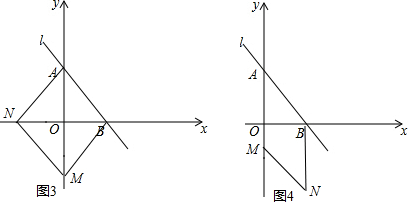
解得,x1=5
-5,x2=5
+5(舍去),
答:CF的长为5
-5;
(3)如图3,四边形ANMB为菱形,
点N的坐标为(-3,0),
如图4,四边形AMNB为菱形,
则BN=AB=5,
点N的坐标为(3,-5),
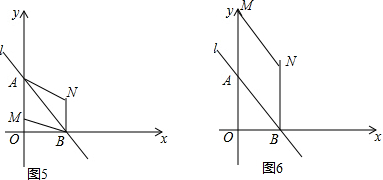
如图5,四边形AMBN为菱形,
设AM=x,则BM=x,OM=4-x,
由勾股定理得,BM2=OM2+OB2,即x2=(4-x)2+32,
解得,x=
,
点N的坐标为(3,
),
如图6,四边形ABNM为菱形,
BN=AB=5,
点N的坐标为(3,5),
以A、B、M、N为顶点的四边形是菱形,N点的坐标为(3,5)或(3,-5)或(-3,0)或(3,
).
x1=3,x2=4,

∵OA>OB,
∴OA=4,OB=3,
由勾股定理得,AB=
| OA2+OB2 |
∴cos∠ABO=
| OB |
| AB |
| 3 |
| 5 |
(2)如图2,过F作FH⊥BC于H,
∵BF是∠CBD的平分线,
∴EF=HF,
又∵四边形ABCD为正方形,
∴EF=HF=CH,又∵AB=5,
∴CE=5sin45°=
5
| ||
| 2 |
设CF=x,则EF=HF=CH=
5
| ||
| 2 |
由勾股定理得,CF2=FH2+HC2,即x2=2(
5
| ||
| 2 |

解得,x1=5
| 2 |
| 2 |
答:CF的长为5
| 2 |
(3)如图3,四边形ANMB为菱形,
点N的坐标为(-3,0),
如图4,四边形AMNB为菱形,
则BN=AB=5,
点N的坐标为(3,-5),
如图5,四边形AMBN为菱形,
设AM=x,则BM=x,OM=4-x,
由勾股定理得,BM2=OM2+OB2,即x2=(4-x)2+32,
解得,x=
| 25 |
| 8 |
点N的坐标为(3,
| 25 |
| 8 |
如图6,四边形ABNM为菱形,
BN=AB=5,
点N的坐标为(3,5),
以A、B、M、N为顶点的四边形是菱形,N点的坐标为(3,5)或(3,-5)或(-3,0)或(3,
| 25 |
| 8 |

看了 如图,在平面直角坐标系中,直...的网友还看了以下:
关于向量的问题设向量a,b是两个不共线的非零向量(t∈R),若向量a的模向=向量b的模,且向量a与 2020-05-14 …
若函数f(x)=x2+ax+b有两个不同的零点x1,x2,且1<x1<x2<3,那么在f(1),f 2020-05-17 …
已知等式(2A-7B)x+(3A-8B)=8x+10对一切实数x都成立,求A,B的值.两超市销售额 2020-06-06 …
已知点A(a,﹣5)、B(8,b),根据下列条件确定a、b的值(1)A、B关于y轴对称(2)A、B 2020-06-14 …
有AB两点,在数轴上分别表示实数a,b,若a的绝对值是b的绝对值的4倍,且A,B两点间的距离是15 2020-06-20 …
若实数a,b满足a+3b=m(m为整数),请按要求回答下列问题:(1)若m=2,且a,b都是整数, 2020-07-22 …
在△ABC中,a=4,A=30°(1)请你给出一个b值,使该三角形有唯一解(2)请你给出一个b值, 2020-07-27 …
下列各命题的逆命题不成立的是()A.两直线平行,同旁内角互补B.若两个数的绝对值相等,则这两个数也 2020-07-29 …
读等值线分布图,图中数值a>b>c,下列叙述正确的是()A.若是等高线图,①地气温低于同纬度②地气温 2020-11-02 …
如图所示,电阻R和线圈自感系数L的值都较大,电感线圈的电阻不计,A、B是两只完全相同的灯泡,当开关S 2020-11-08 …