早教吧作业答案频道 -->数学-->
在半圆O中,AB为直径,弦AD、BC交于E,连接CD,∠C+2∠D=90°.(1)如图1,求证:弧AC=弧CD;(2)如图2,点F为劣弧BD上一点,连接OF交BC于G,连接BF,若∠CBF=45°,求证:BG=EG;(3)如图3,在
题目详情
在半圆O中,AB为直径,弦AD、BC交于E,连接CD,∠C+2∠D=90°.
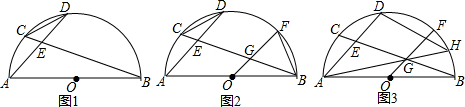
(1)如图1,求证:弧AC=弧CD;
(2)如图2,点F为劣弧BD上一点,连接OF交BC于G,连接BF,若∠CBF=45°,求证:BG=EG;
(3)如图3,在(2)的条件下,连接AG并延长与 O相交于点H,连接DH,若HG=5,DH=9,求线段BE的长度.

(1)如图1,求证:弧AC=弧CD;
(2)如图2,点F为劣弧BD上一点,连接OF交BC于G,连接BF,若∠CBF=45°,求证:BG=EG;
(3)如图3,在(2)的条件下,连接AG并延长与 O相交于点H,连接DH,若HG=5,DH=9,求线段BE的长度.
▼优质解答
答案和解析
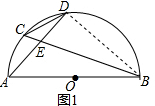 (1)连接BD,
(1)连接BD,
∵AB为 O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠C+2∠D=90°,∠A=∠C,
∴∠ABD=2∠ADC,
∵∠ADC=∠ABC,
∴∠ABC=∠CBD,
∴
=
;
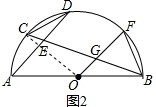
(2)连接OC,
∵∠CBF=45°,
∴∠COF=90°,
∵
=
,
∴OC⊥AD,
∴AD∥OF,
∵AO=BO,
∴BG=EG;
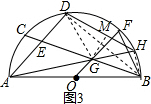
(3)连接BD,DG,作GM⊥DH于M,
∵AB为 O的直径,
∴∠ADB=90°,
∵BG=EG,
∴DG=BG,
∵∠GDM=∠GDB+∠BDH,∠BGH=∠GBA+∠HAB,
∵∠BDH=∠BAH,∠GDB=∠GBD,
∴∠GDM=∠BGH,
在△DGM与△BGH中,
,
∴△DGM≌△BGH,
∴DM=HG,
∵HG=5,DH=9,
∴MH=4,
∴MG=
=3,
∴DG=
=
,
∴BG=DG=
,
∴BE=2BG=2
.
 (1)连接BD,
(1)连接BD,∵AB为 O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠C+2∠D=90°,∠A=∠C,
∴∠ABD=2∠ADC,
∵∠ADC=∠ABC,
∴∠ABC=∠CBD,
∴
 |
| AC |
 |
| CD |

(2)连接OC,
∵∠CBF=45°,
∴∠COF=90°,
∵
 |
| AC |
 |
| CD |
∴OC⊥AD,
∴AD∥OF,
∵AO=BO,
∴BG=EG;

(3)连接BD,DG,作GM⊥DH于M,
∵AB为 O的直径,
∴∠ADB=90°,
∵BG=EG,
∴DG=BG,
∵∠GDM=∠GDB+∠BDH,∠BGH=∠GBA+∠HAB,
∵∠BDH=∠BAH,∠GDB=∠GBD,
∴∠GDM=∠BGH,
在△DGM与△BGH中,
|
∴△DGM≌△BGH,
∴DM=HG,
∵HG=5,DH=9,
∴MH=4,
∴MG=
| GH2-MH2 |
∴DG=
| DM2+MG2 |
| 34 |
∴BG=DG=
| 34 |
∴BE=2BG=2
| 34 |
看了 在半圆O中,AB为直径,弦A...的网友还看了以下:
已知点p在曲线8/(e^x+2)上,α为曲线在点p处的切线的倾斜角,则α的取值范围A[0,π/4] 2020-04-11 …
如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).与线段BC交于点D,直线y=-1 2020-05-16 …
水排空的时间A.1~1.5小时 B.1.5~2小时 C.2~3小时 D.3~4小时 E.4~6小时 2020-06-04 …
母乳排空的时间A.1~1.5小时 B.1.5~2小时 C.2~3小时 D.3~4小时 E.4~6小时 2020-06-04 …
牛乳排空的时间A.1~1.5小时 B.1.5~2小时 C.2~3小时 D.3~4小时 E.4~6小时 2020-06-04 …
在平面直角坐标系内画出下列各点:A(2,1),B(4,1),C(-1,3),D(-1,5),E(3 2020-07-31 …
超急!只限今天,100分!好的再加!(完整形式作答,除了负数除法)A.(-3)/(+6)B.(-5 2020-07-31 …
函数f(x)=xlnx(x>0)的单调区间是若z=sinθ-1/2+icosθ是纯虚数,则TANθ 2020-08-01 …
一个栈的入栈序列是{1,2,3,4,5},在各种出栈序列中,以3,4开头的输出序列可能是______ 2020-12-05 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …