早教吧作业答案频道 -->数学-->
已知函数f(x)=2-|x|,x≤2(x-2)2,x>2,函数g(x)=b-f(2-x),其中b∈R,若函数y=f(x)-g(
题目详情
已知函数f(x)=
,函数g(x)=b-f(2-x),其中b∈R,若函数y=f(x)-g(x)恰好有四个零点,则b的取值范围是___.
| |
|
▼优质解答
答案和解析
∵f(x)=
,
∴f(2-x)=
,
∵函数y=f(x)-g(x)恰好有四个零点,
∴方程f(x)-g(x)=0有四个解,
即f(x)+f(2-x)-b=0有四个解,
即函数y=f(x)+f(2-x)与y=b的图象有四个交点,
y=f(x)+f(2-x)=
,
作函数y=f(x)+f(2-x)与y=b的图象如下,
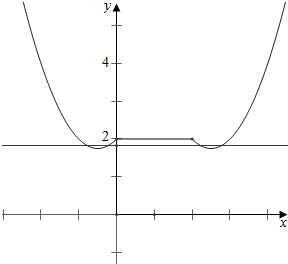 ,
,
f(
)+f(2-
)=f(
)+f(2-
)=
,
结合图象可知,
<b<2,
故答案为:(
,2).
|
∴f(2-x)=
|
∵函数y=f(x)-g(x)恰好有四个零点,
∴方程f(x)-g(x)=0有四个解,
即f(x)+f(2-x)-b=0有四个解,
即函数y=f(x)+f(2-x)与y=b的图象有四个交点,
y=f(x)+f(2-x)=
|
作函数y=f(x)+f(2-x)与y=b的图象如下,
 ,
,f(
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 7 |
| 4 |
结合图象可知,
| 7 |
| 4 |
故答案为:(
| 7 |
| 4 |
看了 已知函数f(x)=2-|x|...的网友还看了以下:
已知3f(x)+2f(x)=x,求f(x)怎么算我自己算了一半因为3f(x)+2f(x)=x3f( 2020-06-03 …
用[x]表示不超过x的最大整数,记{x}=x-[x],其中x∈R,设f(x)=[x]•{x}.用[ 2020-06-04 …
若F(x)=g(x)*f(x)为偶函数且函数y=g(x)为奇函数,则请写出一个符合条件的函数y=f 2020-06-06 …
导数相关的题.1.当K取何值时,分段函数:x不等于0时,f(x)=x的k次方乘以sin(1/x), 2020-06-11 …
求函数的驻点f'x(x,y)=2xy(4-x-y)-x^2y=0.(1)其中f'x(x,y)中左边 2020-07-11 …
导数乘法证明中h是什么意思?(f(x)g(x))'=lim(h→0)[f(x+h)g(x+h)-f 2020-07-22 …
F(x)=x(e^x-1)-ax^2,若当x≥0时f(x)≥0,求a的取值范围?f(xF(x)=x 2020-07-26 …
已知函数f(x)=lnxa+x在x=1处的切线方程为2x-y+b=0.(Ⅰ)求实数a,b的值;(Ⅱ 2020-07-31 …
若函数f(x),g(x)的定义域都是R,则f(x)>g(x)(x∈R)的充要条件是?A.存在一个属 2020-08-02 …
我快死了……函数的一般表达式是什么?是不是y=f(x)(x∈A)?f是某个对应关系,那么这个f(x) 2020-11-01 …