早教吧作业答案频道 -->数学-->
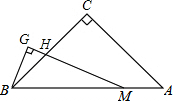
如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=12∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=cm.
题目详情
如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=
∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=___cm.
| 1 |
| 2 |

▼优质解答
答案和解析
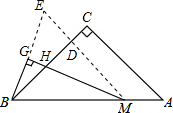 如图,作MD⊥BC于D,延长MD交BG的延长线于E,
如图,作MD⊥BC于D,延长MD交BG的延长线于E,
∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠A=45°,
∵∠GMB=
∠A,
∴∠GMB=
∠A=22.5°,
∵BG⊥MG,
∴∠BGM=90°,
∴∠GBM=90°-22.5°=67.5°,
∴∠GBH=∠EBM-∠ABC=22.5°.
∵MD∥AC,
∴∠BMD=∠A=45°,
∴△BDM为等腰直角三角形
∴BD=DM,
而∠GBH=22.5°,
∴GM平分∠BMD,
而BG⊥MG,
∴BG=EG,即BG=
BE,
∵∠MHD+∠HMD=∠E+∠HMD=90°,
∴∠MHD=∠E,
∵∠GBD=90°-∠E,∠HMD=90°-∠E,
∴∠GBD=∠HMD,
∴在△BED和△MHD中,
,
∴△BED≌△MHD(AAS),
∴BE=MH,
∴BG=
MH=4.
故答案是:4.
 如图,作MD⊥BC于D,延长MD交BG的延长线于E,
如图,作MD⊥BC于D,延长MD交BG的延长线于E,∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠A=45°,
∵∠GMB=
| 1 |
| 2 |
∴∠GMB=
| 1 |
| 2 |
∵BG⊥MG,
∴∠BGM=90°,
∴∠GBM=90°-22.5°=67.5°,
∴∠GBH=∠EBM-∠ABC=22.5°.
∵MD∥AC,
∴∠BMD=∠A=45°,
∴△BDM为等腰直角三角形
∴BD=DM,
而∠GBH=22.5°,
∴GM平分∠BMD,
而BG⊥MG,
∴BG=EG,即BG=
| 1 |
| 2 |
∵∠MHD+∠HMD=∠E+∠HMD=90°,
∴∠MHD=∠E,
∵∠GBD=90°-∠E,∠HMD=90°-∠E,
∴∠GBD=∠HMD,
∴在△BED和△MHD中,
|
∴△BED≌△MHD(AAS),
∴BE=MH,
∴BG=
| 1 |
| 2 |
故答案是:4.
看了 如图,△ABC中,∠C=90...的网友还看了以下:
把一副三角尺(30°,60°,90°,和45°,45°,90°)如图(甲)放置在平面直角坐标系中, 2020-04-13 …
求解答:matlab中分段函数问题symsuf=-2*u.^4+2*u.^2+u/6+0.3;if 2020-05-12 …
该患儿L-甲状腺素(优甲乐)一般推举维持量为A.6/μg/(kg·d)B.7/xg/(kg·d)C. 2020-06-06 …
某病人的血浆、尿液成分化验如下:成分样品A、(g/100ml(液体)样品B、(g/100ml(液体 2020-06-26 …
设G是一个非空集合,*是定义在G上的一个运算.如果同时满足下述四个条件:(ⅰ)对于∀a,b∈G,都 2020-08-01 …
送分某电话号码格式如ABC-DEF-GHIJ,每个字母代表的数字不同.A>B>C且D>E>F且G> 2020-08-02 …
高者来答!若a=2cm,b=8cm,则a,b,b-a的若a=2cm,b=8cm,则a,b,b-a的 2020-08-02 …
三元一次方程组a*x+b*y+c*z+d=0,e*x+f*y+g*z+h=0,i*x+j*y+k* 2020-08-03 …
若函数f(x)=|x2-k|的图象与函数g(x)=x-3的图象至多有一个公共点,则实数k的取值范围是 2020-12-14 …
物体自由落体运动方程为s(t)=12gt2,若limn→∞s(1+△t)−s(1)△t=g=9.8m 2021-01-22 …