早教吧作业答案频道 -->数学-->
如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.
题目详情
如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=
30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.
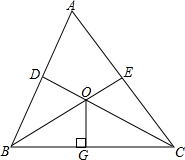
30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.

▼优质解答
答案和解析
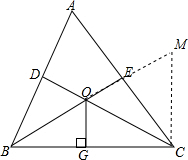 证明:延长OE至点M,使OM=OC,连接CM,
证明:延长OE至点M,使OM=OC,连接CM,
∵∠BCD=∠CBE=30°,
∴OB=OC,∠MOC=30°+30°=60°,
∵OM=OC,
∴△OMC为等边三角形,
∴CM=OC=OB,∠M=60°,
∴∠DBO=∠MCE,
在△BOD和△CME中,
,
∴△BOD≌△MCE,
∴DO=EM,
∴OE+OD=OM=OB,
在Rt△OBG中,∠OBG=30°,OG⊥BC,
∴2OG=OB,
∴OE+OD=2OG.
 证明:延长OE至点M,使OM=OC,连接CM,
证明:延长OE至点M,使OM=OC,连接CM,∵∠BCD=∠CBE=30°,
∴OB=OC,∠MOC=30°+30°=60°,
∵OM=OC,
∴△OMC为等边三角形,
∴CM=OC=OB,∠M=60°,
∴∠DBO=∠MCE,
在△BOD和△CME中,
|
∴△BOD≌△MCE,
∴DO=EM,
∴OE+OD=OM=OB,
在Rt△OBG中,∠OBG=30°,OG⊥BC,
∴2OG=OB,
∴OE+OD=2OG.
看了 如图,△ABC中,∠BAC=...的网友还看了以下:
反比例函数图像Y=K/X的图像经过点M[a,b]和点N[c,d],如果a大于c大于0,则0小于b小 2020-04-08 …
如图,△ABC中,点O在边AB上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⊥BD 2020-04-09 …
菱形ABCD的两条对角线相交于点O,AC=4.2,BD=3,分别在线段OA,OB.OC.OD,上取 2020-05-17 …
对于定义域为D的函数y=f(x),若同时满足下列条件:①f(x)在D内单调递增或单调递减;②存在区 2020-05-23 …
如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于 2020-07-30 …
如果a小于b,c小于a,b小于d,那么下面分数中,最大的一个是()A.a3B.b3C.c3D.d3 2020-10-31 …
高三学渣悔改求学.设f(x)的定义域为D,若f(x)满足条件:存在[a,b]属于D使为什么在x=a时 2020-11-04 …
有字符串A="1,2,,3,4,5,4",B=",4,5,Aaa,测试,9”利用C#技术如何做出以下 2020-11-07 …
若a/b大于或等于c/d,那么从b小于d能否推出a大于c 2020-11-08 …
救急.急!在三角形ABC中,角B,角C平分线交于点D,OD垂直BC于D,如果AB等于15厘米,BC等 2020-12-19 …