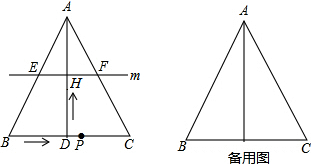
如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，

Question

如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t>0）．
（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；
（2）当t=2时，求△PEF的面积；
（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值；若不存在，请说明理由．

Answer 1

（1）证明：∵AB=AC，AD⊥BC，
∴∠BAD=∠CAD，又直线m垂直于AD，
∴AD垂直平分EF，
当t=2时，DH=4，又AD=8，
∴AH=HD，
则AD与EF垂直平分，
∴四边形AEDF为菱形；
（2） ∵m∥BC，
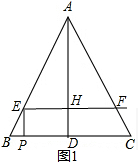
∴△AEF∽△ABC，
∴(EF)/(BC)=(AH)/(AD)，
∴EF=(1)/(2)BC=5，
∴△PEF的面积=(1)/(2)×EF×DH=10cm²；
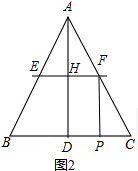
（3） 如图1，当PE⊥EF时，
由题意得，BP=3t，PE=2t，
∵PE⊥EF，AD⊥BC，
∴EP∥AD，
∴(BP)/(BD)=(EP)/(AD)，即(3t)/(5)=(2t)/(8)，
则t不存在；
如图2，当PF⊥EF时，
PF=2t，CP=10-3t，
∵PF∥AD，
∴(PF)/(AD)=(CP)/(CD)，即(10-3t)/(5)=(2t)/(8)，
解得t=(40)/(17)，
∴当t=(40)/(17)时，△PEF为直角三角形．
如图3，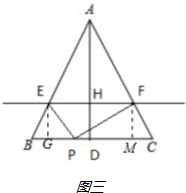
当EP⊥FP时，分别过E、F作BC的垂线，垂足分别是G、M．
由于EF平行BC，又因为∠EGP=∠FPE=∠PMF=90°
故易证△EGP∽△FPE∽△PMF；
又△BGE∽△BDA，EG=2t，故可以求得BG=(5)/(4)t，从而GP=BP-BG=(7)/(4)t，
由等腰三角形的对称性可知，CM=(5)/(4)t，从而PM=BC-BP-MC=10-(17)/(4)t；
因为△EGP∽△PMF，有(EG)/(PM)=(GP)/(MF)，分别代入数据，
有(2t)/(10-(17)/(4)t)=((7)/(4)t)/(2t)
整理得((183)/(16)t-(70)/(4))t=0，故t=0（舍去），t=(280)/(183)
综上当t=(40)/(17)或(280)/(183)