早教吧作业答案频道 -->数学-->
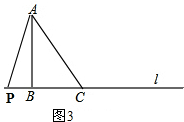
如图,Rt△ACB在直线l上,且∠ABC=90°,BC=6cm,AC=10cm.(1)求AB的长.(2)若有一动点P从点B出发,以2cm/s的速度在直线l上运动,则当t为何值时,△ACP为等腰三角形?
题目详情
如图,Rt△ACB在直线l上,且∠ABC=90°,BC=6cm,AC=10cm.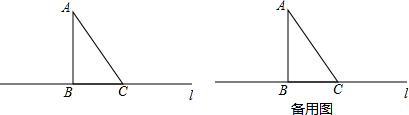
(1)求AB的长.
(2)若有一动点P从点B出发,以2cm/s的速度在直线l上运动,则当t为何值时,△ACP为等腰三角形?
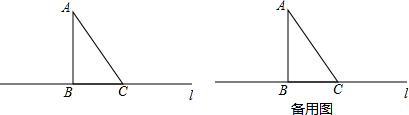
(1)求AB的长.
(2)若有一动点P从点B出发,以2cm/s的速度在直线l上运动,则当t为何值时,△ACP为等腰三角形?
▼优质解答
答案和解析
(1)∵∠ABC=90°,BC=6cm,AC=10cm,
∴AB=
=
=8cm;
(2)①如图1,若CP=CA,
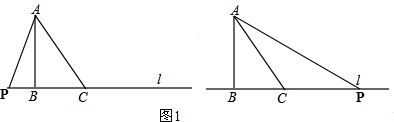
则:BP=CP+BC=6+10=16或BP=CP-BC=10-6=4,
即2t=16,t=8或2t=4,t=2;
②如图2,若AP=AC,
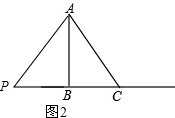
则:AB垂直平分PC,BP=BC=6,
即2t=6,t=3;
③若PA=PC,
则P在AC的垂直平分线上,所以P在B左侧,
PB=2t,BC=6,
∴t=8,PA=2t+6,
∵∠ABP=90°,
∴AP2=AB2+BP2,
即(2t+6)2=(2t)2+82,
解得t=
;
综上所述,当点P向左运动
s、2s、3s或向右运动8s时,△ACP为等腰三角形.
∴AB=
| AC2-BC2 |
| 102-62 |
(2)①如图1,若CP=CA,

则:BP=CP+BC=6+10=16或BP=CP-BC=10-6=4,
即2t=16,t=8或2t=4,t=2;
②如图2,若AP=AC,

则:AB垂直平分PC,BP=BC=6,
即2t=6,t=3;
③若PA=PC,

则P在AC的垂直平分线上,所以P在B左侧,
PB=2t,BC=6,
∴t=8,PA=2t+6,
∵∠ABP=90°,
∴AP2=AB2+BP2,
即(2t+6)2=(2t)2+82,
解得t=
| 7 |
| 6 |
综上所述,当点P向左运动
| 7 |
| 6 |
看了 如图,Rt△ACB在直线l上...的网友还看了以下:
下列词语中加点字的读音;全都正确的—组是A.发霉(méi)懊悔(huǐ)欺侮(rǔ)风雨如晦(hu 2020-05-13 …
已知m.l是直线,α.β是平面,则下列命题正确的是()A.若l平行于α,则l平行于α内的所有直线B 2020-05-15 …
已知m,l,n是直线,α,β是平面,下列命题中正确的是()A.若m⊄α,l⊂α则m∥lB.若l⊥α 2020-07-15 …
已知l,m,n是三条不同的直线,α,β是不同的平面,则α⊥β的一个充分条件是()A.lα,mβ,且 2020-07-26 …
已知直线l、m,平面a、b,且l⊥a,mÌb,给出下列四个命题;(1)若a∥b,则l⊥m.(2)若l 2020-11-02 …
设l,m是两条不同的直线,a是一个平面,则下列命题正确的是()A.若l⊥m,m⊂a,则l⊥aB.若l 2020-11-02 …
设l,m,n为三条不同的直线,a为一个平面,对于下列命题:①若l⊥a,则l与a相交;②若m⊂a,n⊂ 2020-11-02 …
已知直线l、m,平面a、b,且l⊥a,mìb,给出下列四个命题;(1)若a∥b,则l⊥m.(2)若l 2020-11-02 …
关于直线a,b,l以及平面M,N,下面命题中正确的是()A.若a∥M,b∥M,则a∥bB.若a∥M, 2020-11-02 …
已知点M(a,b)(ab≠0)是圆x2+y2=r2内一点,直线m是以点M为中点的弦所在的直线,直线l 2020-11-02 …