早教吧作业答案频道 -->数学-->
如图,已知△ABC中,∠ACB=90°,∠ABC=30°,AC=2,点P是边AB上的一个动点,以点P为圆心,PB的长为半径画弧,交射线BC于点D,射线PD交射线AC于点E.(1)当点D与点C重合时,求PB的长;(2)当点
题目详情
如图,已知△ABC中,∠ACB=90°,∠ABC=30°,AC=2,点P是边AB上的一个动点,以点P为圆心,PB的长为半径画弧,交射线BC于点D,射线PD交射线AC于点E.
(1)当点D与点C重合时,求PB的长;
(2)当点E在AC的延长线上时,设PB=x,CE=y,求y关于x的函数关系式,并写出定义域;
(3)当△PAD是直角三角形时,求PB的长.
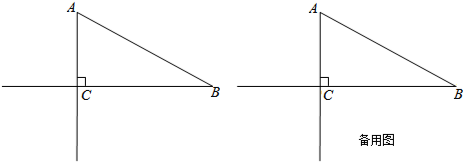
(1)当点D与点C重合时,求PB的长;
(2)当点E在AC的延长线上时,设PB=x,CE=y,求y关于x的函数关系式,并写出定义域;
(3)当△PAD是直角三角形时,求PB的长.

▼优质解答
答案和解析
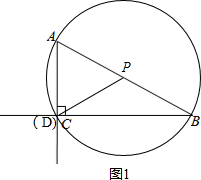 (1)如图1,∵在△ABC 中,∠ACB=90°,∠ABC=30°,
(1)如图1,∵在△ABC 中,∠ACB=90°,∠ABC=30°,
∴AC=
AB,
∵AC=2,
∴AB=4,
∵以点P为圆心,PB的长为半径画弧,交射线BC于点D,点D与点C重合,
∴PD=PB,
∴∠PCB=∠B=30°,
∴∠APC=∠ACD=60°,
∴AP=AC=2,
∴BP=2;
(2)∵PD=PB,∠ABC=30°,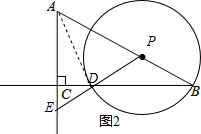
∴∠PDB=∠B=30°,
∴∠APE=60°,∠CDE=30°,
∵∠ACD=90°,
∴∠AEP=60°,
∴AE=AP,
∵PB=x,CE=y,
∴2+y=4-x,y=2-x.(0<x<2);
(3)①如图2,当点E在AC的延长线上时,连接AD,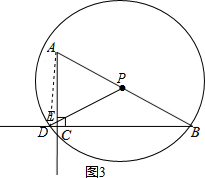
∵△PAD是直角三角形,∠APD=60°,∠PAD<60°,
∴∠PDA=90°,
∴∠PAD=30°.
∴PD=
AP,
即x=
(4-x),
∴x=
;
②如图3,当点E在AC边上时,连接AD
∵△PAD是直角三角形,∠APD=60°,∠ADP<60°,
∴∠PAD=90°,
∴∠PDA=30°.
∴AP=
PD.即4-x=
x,
∴x=
.
综上所述:当PB的长是
或
时,△PAD是直角三角形.
 (1)如图1,∵在△ABC 中,∠ACB=90°,∠ABC=30°,
(1)如图1,∵在△ABC 中,∠ACB=90°,∠ABC=30°,∴AC=
| 1 |
| 2 |
∵AC=2,
∴AB=4,
∵以点P为圆心,PB的长为半径画弧,交射线BC于点D,点D与点C重合,
∴PD=PB,
∴∠PCB=∠B=30°,
∴∠APC=∠ACD=60°,
∴AP=AC=2,
∴BP=2;
(2)∵PD=PB,∠ABC=30°,

∴∠PDB=∠B=30°,
∴∠APE=60°,∠CDE=30°,
∵∠ACD=90°,
∴∠AEP=60°,
∴AE=AP,
∵PB=x,CE=y,
∴2+y=4-x,y=2-x.(0<x<2);
(3)①如图2,当点E在AC的延长线上时,连接AD,

∵△PAD是直角三角形,∠APD=60°,∠PAD<60°,
∴∠PDA=90°,
∴∠PAD=30°.
∴PD=
| 1 |
| 2 |
即x=
| 1 |
| 2 |
∴x=
| 4 |
| 3 |
②如图3,当点E在AC边上时,连接AD
∵△PAD是直角三角形,∠APD=60°,∠ADP<60°,
∴∠PAD=90°,
∴∠PDA=30°.
∴AP=
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
| 8 |
| 3 |
综上所述:当PB的长是
| 4 |
| 3 |
| 8 |
| 3 |
看了 如图,已知△ABC中,∠AC...的网友还看了以下:
在直角坐标系中,椭圆C:X^2/a^2+y^2/b^2=1,圆O:x^2+y^2=a^2,且过点A 2020-05-16 …
已知椭圆E:x^2/a^2+y^2/b^2=1(a>b>0)的离心率为1/2,直线x=2被椭圆E截 2020-05-16 …
抛物线y=-x2+2x+3与x轴相交于a,b两点,点a在b的左边,与y轴相交于点c,抛物线顶点为d 2020-05-16 …
已知椭圆方程为x^2/a^2+y^2/b^2=1(a>b>0),过椭圆焦点F(c,0)的直线与椭圆 2020-05-23 …
已知圆C:x^2+(y-a)^2=4,点A(1,0),其中a是常数,当过点A的圆C的切线存在时(1 2020-06-09 …
如图,已知点A(2,0),点B在y轴正半轴上,且OB=1/2OA,将点B绕点A顺时针方向旋转90度 2020-06-13 …
1)a、b、C为三角形ABC的内角,所对的边分别为a、b、c、且(a^2+c^2-b^2)/(a^ 2020-06-13 …
已知椭圆C:X^2/2+y^2=1的右焦点为F,右准线为L,点A∈L,线段AF交C于点B,若向量F 2020-06-30 …
关于椭圆的问题设A、B是椭圆x^2/a^2+y^2/b^2=1(a>b>0)的长轴的两端点,P是椭 2020-07-21 …
已知x^2/a^2+y^2/b^2=1(a>b>0)的两焦点为F1(-c,0),F2(c,0),P是 2020-11-01 …