早教吧作业答案频道 -->数学-->
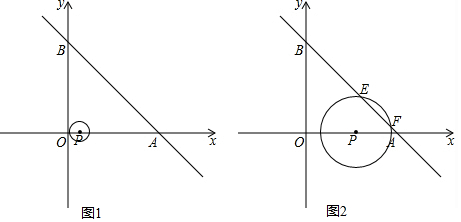
如图1,一次函数y=-x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时P的半径以每秒增加1个单位的速度不断变大,设运动
题目详情
如图1,一次函数y=-x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的 P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时 P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为___,点B的坐标为___,∠OAB=___°;
(2)在运动过程中,点P的坐标为___, P的半径为___(用含t的代数式表示);
(3)当 P与直线AB相交于点E、F时
①如图2,求t=
时,弦EF的长;
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
(1)点A的坐标为___,点B的坐标为___,∠OAB=___°;
(2)在运动过程中,点P的坐标为___, P的半径为___(用含t的代数式表示);
(3)当 P与直线AB相交于点E、F时
①如图2,求t=
| 5 |
| 2 |
②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).

▼优质解答
答案和解析
(1)∵y=-x+10的图象交x轴于点A,交y轴于点B,
∴A(10,0),B(0,10),
∴OA=OB=10,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
故答案分别为(10,0),(0,10),45°.
(2)由题意P(1+2t,0), O半径为1+t,
故答案分别为(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.
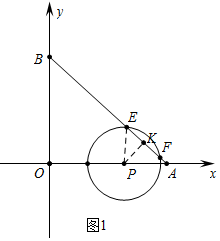
当t=
时,P(6,0),半径为3.5,
在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,
∴PK=
PA=2
,
在Rt△PEK中,EK=
=
,
∴EF=2EK=
.
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°
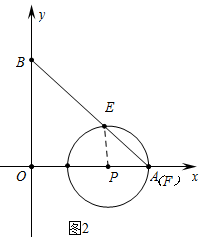
∵OP+PA=OA,
∴1+2t+1+t=10,
∴t=
.
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.
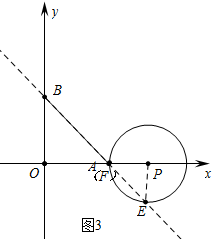
由OP-PF=OA,
∴1+2t-(1+t)=10,
∴t=10,
综上所述,t=
s或10s时,存在以点P为直角顶点的Rt△PEF.
∴A(10,0),B(0,10),
∴OA=OB=10,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
故答案分别为(10,0),(0,10),45°.
(2)由题意P(1+2t,0), O半径为1+t,
故答案分别为(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.

当t=
| 5 |
| 2 |
在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,
∴PK=
| ||
| 2 |
| 2 |
在Rt△PEK中,EK=
| PE2-PK2 |
| ||
| 2 |
∴EF=2EK=
| 17 |
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°

∵OP+PA=OA,
∴1+2t+1+t=10,
∴t=
| 8 |
| 3 |
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.

由OP-PF=OA,
∴1+2t-(1+t)=10,
∴t=10,
综上所述,t=
| 8 |
| 3 |
看了 如图1,一次函数y=-x+1...的网友还看了以下:
数学:关于函数奇偶性f(x)是定义r上的奇函数,且x大于0时,f(x)=2x²-x+3,则当x小于 2020-05-16 …
高三第一轮复习几道关于函数的题!要过陈1.某种货物运输费y元与公里数有如下关系若公里数不超过50公 2020-06-04 …
对于函数f(x)=(ax+1)/(x-1),其中a为实数,x不等于1,给出下列命题(1)、a=1时 2020-07-01 …
关于函数的定义的问题.函数的定义说对于每个在定义域的自变量,都只有一个因变量与之相对应,那么,一个 2020-07-25 …
关于函数的疑问,先看关于函数的定义:一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每 2020-07-30 …
周期函数的定义问题周期函数的定义:对于函数y=f(x),如果存在一个不为零的常数T,使得当x取定义 2020-07-30 …
关于三角函数周期的问题如果存在一个不等于零的常数T,对于函数y=f(x)使得当x取定义域内的每一个 2020-08-02 …
一道函数题设A是由26个英文字母组成的集合,设B={0,1,2,...,24,25}对应法则f为f 2020-08-02 …
怎么证明一个函数的不动点包含稳定点对于函数f(x),若有f(x)=x则称x为该函数的"不动点",若f 2020-10-30 …
怎么能一眼看出来极限?还有个方法,非常方便的方法就是当趋近于无穷大时候不同函数趋近于无穷的速度是不一 2020-11-06 …