早教吧作业答案频道 -->数学-->
O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.(1)如图(1),若∠AOB=130°,求∠EOF的度数;(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;(3)若∠AOB=α,0°<α<90°,请在图(2)中
题目详情
O为直线DA上一点,OB⊥OF,EO是∠AOB的平分线.
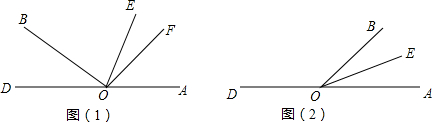
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
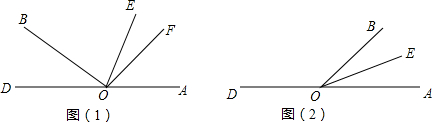
(1)如图(1),若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数;
(3)若∠AOB=α,0°<α<90°,请在图(2)中画出射线OF,使得(2)中∠EOF的结果仍然成立.
▼优质解答
答案和解析
(1)∵∠AOB=130°,EO是∠AOB的平分线,
∴∠AOE=
∠AOB=
×130°=65°,
∵OB⊥OF,
∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴∠EOF=∠AOE-∠AOF=65°-40°=25°;
(2)∵∠AOB=α,90°<α<180°,EO是∠AOB的平分线,
∴∠AOE=
α,
∵∠BOF=90°,
∴∠AOF=α-90°,
∴∠EOF=∠AOE-∠AOF=
α-(α-90°)=90°-
α;
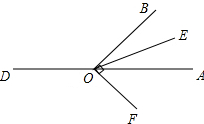
(3)如图,∵∠AOB=α,0°<α<90°,
∴∠BOE=∠AOE=
α,
∵∠BOF=90°,
∴∠EOF=∠BOF-∠BOE=90°-
α.
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵OB⊥OF,
∴∠BOF=90°,
∴∠AOF=∠AOB-∠BOF=130°-90°=40°,
∴∠EOF=∠AOE-∠AOF=65°-40°=25°;
(2)∵∠AOB=α,90°<α<180°,EO是∠AOB的平分线,
∴∠AOE=
| 1 |
| 2 |
∵∠BOF=90°,
∴∠AOF=α-90°,
∴∠EOF=∠AOE-∠AOF=
| 1 |
| 2 |
| 1 |
| 2 |

(3)如图,∵∠AOB=α,0°<α<90°,
∴∠BOE=∠AOE=
| 1 |
| 2 |
∵∠BOF=90°,
∴∠EOF=∠BOF-∠BOE=90°-
| 1 |
| 2 |
看了 O为直线DA上一点,OB⊥O...的网友还看了以下:
设A为实对称矩阵,若A^2=O,则A=O 2020-04-05 …
关于求逆的.设方阵A满足方程A的平方-A-2E=O(opq的o欧),证明:A及A+2E均可逆,并求 2020-04-27 …
平面内有两个定点O(0,0)A(2,0)设点M到O的距离为d1,到A的距离为d2,且d1/d2=根 2020-05-17 …
在自然光线下,瞳孔扩展是指瞳孔的直径为( )A. 2.O~ 3.5mmB. 2.5~ 4.0mmC. 2020-06-07 …
对容量为n的样本,求概率密度f(x,a)=2(a-x)/a^2,o 2020-06-08 …
线性代数AAT相乘的结果?若实对称矩阵A满足A^2=O,证明A=O解答:设A=[aij]n*n则A 2020-06-10 …
设A为实方针,证明(1)如果A=At(转置矩阵),且A^2=O,则A=O;(2)如果A*AT=O, 2020-06-22 …
线形代数高手请进设A为实对称矩阵,A^2=O,求证A=O.要求1.思路清晰2.表达清晰唉,我怎么就 2020-07-18 …
n阶方阵A满足A^2=O,E是n阶单位阵,则A.|E-A|≠0,但|E+A|=0B|E-An阶方阵A 2020-11-02 …
1.若集合A={x|(a-1)x^2+2x+1=o}中只含有一个元素,求实数a2.已知集合A={1, 2020-12-07 …