早教吧作业答案频道 -->数学-->
如图,在四边形OACB中,CM⊥OA于M,∠1=∠2,CA=CB.求证:(1)∠3+∠4=180°;(2)OA+OB=2OM.
题目详情
如图,在四边形OACB中,CM⊥OA于M,∠1=∠2,CA=CB.求证:
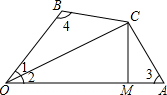
(1)∠3+∠4=180°;
(2)OA+OB=2OM.

(1)∠3+∠4=180°;
(2)OA+OB=2OM.
▼优质解答
答案和解析
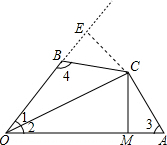 证明:作CE⊥OB于E,
证明:作CE⊥OB于E,
∵CM⊥OA,
∴∠CEB=∠CMA=90°,
又∵∠1=∠2,
∴CE=CM,
在Rt△ECB和Rt△MCA中,
,
∴Rt△ECB≌Rt△MCA(HL),
∴∠3=∠EBC,BE=AM,
在Rt△ECO和Rt△MCO中,
,
∴Rt△ECO≌Rt△MCO(HL),
∴EO=OM,
∵∠EBC+∠4=180°,
∴∠3+∠4=180°;
∴OA+OB=OM+AM+BO=OM+EB+BO=2OM.
 证明:作CE⊥OB于E,
证明:作CE⊥OB于E,∵CM⊥OA,
∴∠CEB=∠CMA=90°,
又∵∠1=∠2,
∴CE=CM,
在Rt△ECB和Rt△MCA中,
|
∴Rt△ECB≌Rt△MCA(HL),
∴∠3=∠EBC,BE=AM,
在Rt△ECO和Rt△MCO中,
|
∴Rt△ECO≌Rt△MCO(HL),
∴EO=OM,
∵∠EBC+∠4=180°,
∴∠3+∠4=180°;
∴OA+OB=OM+AM+BO=OM+EB+BO=2OM.
看了 如图,在四边形OACB中,C...的网友还看了以下:
设函数fn(x)=xn+bx+c(n∈N+,b,c∈R)(1)设n≥2,b=1,c=-1,证明:设函 2020-03-30 …
不等式误区a,b,c都为正,a+b+c=1求1/a^2+1/b^2+1/c^2的最小值帮我看一下我 2020-06-06 …
1.已知a,b,c∈R.a+b+c=1a²+b²+c²=1/2求证c≥02(1)已知a,c是正实数 2020-07-14 …
关于x的方程x+1/x=c+1/c的解是x1=c,x2=1/c;x-1/x=c-c/1(即x+(- 2020-07-21 …
数列{an}的前n项和为sn,且sn=(c+1)-can,(c不等于0,c不等于-1)数列{an} 2020-07-23 …
1.已知a,b,c满足ab+a+b=bc+b+c=ca+c+a=3求(a+1)(b+1(c+1)的 2020-08-01 …
(1)已知a+b=-c,则a(1/a+1/b)+b(1/a+1/c)+c(1/a+1/b)的值是多少 2020-10-31 …
证明组合性质:C(n+1,m)=C(n,m)+C(n,m-1)C(n+1,m)=(n+1)!/m!( 2020-11-01 …
设a、b、c为正数,且a^2+b^2+c^2=3,证明:1/(1+2ab)+1/(1+2bc)+1/ 2020-11-06 …
已知a,b,c为三个互不相等的数,且满足a+1/b=b+1/c=c+1/a=x,求x的值.题文中的a 2020-11-08 …