早教吧作业答案频道 -->数学-->
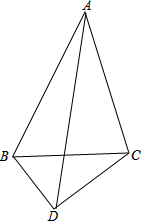
如图,∠BAC=45°,BD:DC:BC=3:4:5,AD=4,∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,求四边形ABCD的面积.
题目详情
如图,∠BAC=45°,BD:DC:BC=3:4:5,AD=4,∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,求四边形ABCD的面积.

▼优质解答
答案和解析
 ∵BD:DC:BC=3:4:5,
∵BD:DC:BC=3:4:5,
∴设BD=3λ,则DC=4λ,BC=5λ;
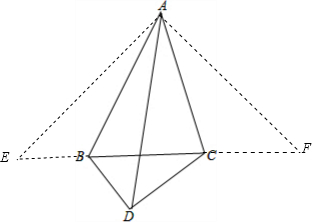
如图,将△ABD、△ACD分别沿AB、AC折叠,得到△ABE和△ACF;
则∠ABE=∠ABD,∠ACD=∠ACF;
AE=AD=4,AF=AD=4;∠EAB=∠DAB,∠FAC=∠DAC;
∵∠BAC=45°,
∴∠EAF=90°
∵∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,
∴∠ABC+∠ABE=180°,∠ACB+∠ACF=180°,
∴E、B、C、F四点共线;
∵∠EAF=90°,
∴△EAF为等腰直角三角形,
∴△AEF的面积=
AE•AF=
×4×4=8;
∵(3λ)2+(4λ)2=(5λ)2,
∴△BDC为直角三角形;
EF=3λ+4λ+5λ=12λ;
由勾股定理得:(12λ)2=42+42,
解得:λ=
,BD=
,DC=
,
∴△BDC的面积=
×
×
=
;
设△ABD、△ADC、△BDC的面积分别为x,y,z;
∵x+y+(x+y)-z=8,而z=
,
∴x+y=
,
即四边形ABCD的面积为
.
 ∵BD:DC:BC=3:4:5,
∵BD:DC:BC=3:4:5,∴设BD=3λ,则DC=4λ,BC=5λ;
如图,将△ABD、△ACD分别沿AB、AC折叠,得到△ABE和△ACF;
则∠ABE=∠ABD,∠ACD=∠ACF;
AE=AD=4,AF=AD=4;∠EAB=∠DAB,∠FAC=∠DAC;
∵∠BAC=45°,
∴∠EAF=90°
∵∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,
∴∠ABC+∠ABE=180°,∠ACB+∠ACF=180°,
∴E、B、C、F四点共线;
∵∠EAF=90°,
∴△EAF为等腰直角三角形,
∴△AEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∵(3λ)2+(4λ)2=(5λ)2,
∴△BDC为直角三角形;
EF=3λ+4λ+5λ=12λ;
由勾股定理得:(12λ)2=42+42,
解得:λ=
| ||
| 3 |
| 2 |
4
| ||
| 3 |
∴△BDC的面积=
| 1 |
| 2 |
| 2 |
4
| ||
| 3 |
| 4 |
| 3 |
设△ABD、△ADC、△BDC的面积分别为x,y,z;
∵x+y+(x+y)-z=8,而z=
| 4 |
| 3 |
∴x+y=
| 14 |
| 3 |
即四边形ABCD的面积为
| 14 |
| 3 |
看了 如图,∠BAC=45°,BD...的网友还看了以下:
在等腰三角形ABC中AB=AC=5,BC=6,点E是BC边上的一点,ED垂直于AB交AB边于点D,E 2020-03-30 …
1.如图,已知在梯形abcd中,ad平行于bc,若两底ad,bc的长分别为2、8,两条对角线bd= 2020-05-15 …
如图,在等腰梯形ABCD中,已知AB//BC,AB=DC,AD=2,BC=4,延长BC到E,使CE 2020-05-16 …
在梯形ABCD中,AD//BC,若AB=DC,E、F分别是CD和BC边上的点,以EF为对称轴翻折梯 2020-05-16 …
在等腰梯形ABCD中,AD╱╱BC,对角线AC⊥BD于O,AE⊥BC,DF⊥BC,垂足分别为E、F 2020-05-16 …
急!求出y与x的函数解析式.(无图)如图,已知底角为45°的等腰梯形ABCD(AD为上底,BC为下 2020-05-24 …
已知△ABC中,边BC的长与BC边上的高的和为20.(1)写出△ABC的面积y与BC的长x之间的函 2020-07-13 …
已知梯形ABCD中,AD//BC,角ABC=角BAD=派/2,AB=BC=2已知在梯形ABCD中, 2020-07-22 …
三角形ABC中,AB=4,BC=5,AC=6,求向量AB·向量BC+向量BC·向量CA+向量CA· 2020-08-02 …
在直角三角形ABCD中,AD//BC,AB⊥BC,AD=6,BC=9,cosC=3/5如图在直角梯形 2020-11-01 …