已知AD与BC是四面体ABCD中相互垂直的棱，若AD=BC=6，且∠ABD=∠ACD=60°，则四面体ABCD的体积的最大值是（）A.182B.362C.18D.36

Question

已知AD与BC是四面体ABCD中相互垂直的棱，若AD=BC=6，且∠ABD=∠ACD=60°，则四面体ABCD的体积的最大值是（　　）

A. 18

√(2)

B. 36

√(2)

C. 18

D. 36

Answer 1

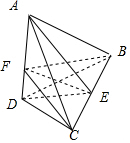过C作CF⊥AD，垂足为F，连接BF，
∵BC⊥AD，CF⊥AD，BC∩CF=C，
∴AD⊥平面BCF，
∴V_A-BCD=(1)/(3)S_△BCF•AD=2S_△BCF．
又∠ACD=∠ABD，AD⊥平面BCF，
∴△ACD≌△ABD，∴CF=BF，
取BC的中点E，则EF⊥BC，
∴2S_△ADE=2×(1)/(2)×BC×EF=6EF，
∴当EF最大时，棱锥的体积取得最大值．
又EF=√(CF2-CE2)=√(CF2-9)，故当CF最大时，棱锥体积最大，
∵∠ACD=60°，AD=6，∴当AC=CD时，CF取得最大值，
此时CF=√(27)=3√(3)，∴EF=3√(2)
∴棱锥的体积最大值为6EF=18√(2)．
故选A．