早教吧作业答案频道 -->数学-->
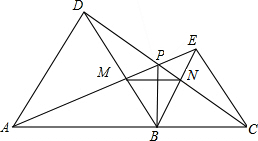
如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分
题目详情
如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有___(填写出所有正确的序号)

▼优质解答
答案和解析
∵△ABD、△BCE均为等边三角形,
∴AB=BD,BE=BC,∠ABD=∠CBE=60°,
∴∠ABE=∠CBD,
在△ABE与△CBD中,
,
∴△ABE≌△DBC,
∴AE=CD,故①正确;
∵△ABE≌△DBC,
∴∠BAP=∠BDC,
∵A、B、C在一条直线上,
∴∠DBN=180°-∠ABD-∠CBE=60°,
∴∠ABD=∠DBN,
在△ABM与△BDN中,
,
∴△ABM≌△DBN,
∴AM=DN,BM=BN,
∵DN>PD,
∴AM>PD,故②错误;
∵BM=BN,∠MBN=60°,
∴△BMN是等边三角形,
∴∠MNB=60°,
∴∠MNB=∠NBC,
∴MN∥AC,故③正确;
取BD的中点O,连接EO,DE,
∵AB=2BC,
∴BD=2BE,
∴BE=BM=DM,
∵∠MBE=60°,
∴△BEM是等边三角形,
∴EM=BM=DM,
∴∠BED=90°,
∴DE⊥BE;故④正确;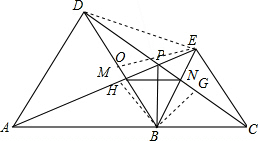
过B作BG⊥CD于G,BH⊥AE于H,
∴∠AHB=∠DGB=90°,
在△ABH与△DBG中,
,
∴△ABH≌△DBG,
∴BH=BG,
∴BP平分∠APC;故⑤正确;
∵当A、B、C在一条直线上时,∠ABM=∠DBN=60°,
∠DBE≠60°,则∠ABM≠∠DBN,
∴△ABM与△DBN不全等,
∴AM≠DN,故⑥错误.
故答案为:①③④⑤.
∴AB=BD,BE=BC,∠ABD=∠CBE=60°,
∴∠ABE=∠CBD,
在△ABE与△CBD中,
|
∴△ABE≌△DBC,
∴AE=CD,故①正确;
∵△ABE≌△DBC,
∴∠BAP=∠BDC,
∵A、B、C在一条直线上,
∴∠DBN=180°-∠ABD-∠CBE=60°,
∴∠ABD=∠DBN,
在△ABM与△BDN中,
|
∴△ABM≌△DBN,
∴AM=DN,BM=BN,
∵DN>PD,
∴AM>PD,故②错误;
∵BM=BN,∠MBN=60°,
∴△BMN是等边三角形,
∴∠MNB=60°,
∴∠MNB=∠NBC,
∴MN∥AC,故③正确;
取BD的中点O,连接EO,DE,
∵AB=2BC,
∴BD=2BE,
∴BE=BM=DM,
∵∠MBE=60°,
∴△BEM是等边三角形,
∴EM=BM=DM,
∴∠BED=90°,
∴DE⊥BE;故④正确;

过B作BG⊥CD于G,BH⊥AE于H,
∴∠AHB=∠DGB=90°,
在△ABH与△DBG中,
|
∴△ABH≌△DBG,
∴BH=BG,
∴BP平分∠APC;故⑤正确;
∵当A、B、C在一条直线上时,∠ABM=∠DBN=60°,
∠DBE≠60°,则∠ABM≠∠DBN,
∴△ABM与△DBN不全等,
∴AM≠DN,故⑥错误.
故答案为:①③④⑤.
看了 如图,A、B、C在一条直线上...的网友还看了以下:
如图所示,烧瓶内有一只活的小白鼠,U形管内装有红色水溶液,a、b两端的液面处于同一水平面.两天后,U 2020-03-31 …
深圳地区经常会有台风,市政府要求居民将简易房的屋顶加固,对于这一要求下列解释正确的是()。A.屋顶 2020-04-07 …
位于西部地区的ab两地据多年的记载ab两地一年中下雨仅占百分之6和百分之8,同时下雨比例百分之2, 2020-04-26 …
当b>a>0时,根号下a的平方分之一-b的平方分之一等于1.根号下a的平方分之一-b的平方分之一等 2020-05-14 …
正交矩阵是否能证明对称,有一题如下 对于任意正交矩阵A,AAT=ATA=E,证明|E-A^2|=0 2020-05-15 …
上面一个于下面一个心念什么字 2020-05-17 …
高一化学烧瓶内有一只活的小白鼠U形管内装有红色水溶液,a、b两端的液面处于同一水平面.两天后,U形 2020-05-20 …
下列关于茶壶醉的设计说法中,正确的是A.壶嘴高于壶口B.壶嘴低于壶口C.壶嘴做的与壶口一样高下列关 2020-06-04 …
各位大师,求解一道初一数学题!ABCD是梯形(左上是B,右上是A,左下是C,右下是D),AB=2, 2020-06-05 …
如图,一物块以1m/s的初速度沿粗糙半圆面由A处下滑,到达较低的B点时速度恰好也是1m/s,如果此 2020-06-16 …