早教吧作业答案频道 -->数学-->
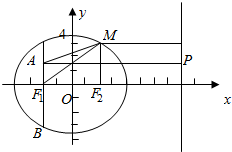
已知点A(-2,3)为椭圆x216+y212=1内一点,F2为其右焦点,M为椭圆上一动点.(1)求|AM|+|MF2|的最大值;(2)求|AM|+2|MF2|的最小值.
题目详情
已知点A(-2,
)为椭圆
+
=1内一点,F2为其右焦点,M为椭圆上一动点.
(1)求|AM|+|MF2|的最大值;
(2)求|AM|+2|MF2|的最小值.
| 3 |
| x2 |
| 16 |
| y2 |
| 12 |
(1)求|AM|+|MF2|的最大值;
(2)求|AM|+2|MF2|的最小值.
▼优质解答
答案和解析
 (1)椭圆
(1)椭圆
+
=1的a=4,b=2
,c=2,
焦点为F1(-2,0),F2(2,0),
由椭圆的第一定义可得|MF1|+|MF2|=2a=8,
|AM|+|MF2|=8+|MA|-|MF1|,
连接AF1,延长交椭圆于B,即有|BA|-|BF1|=|AF1|=
,
此时取得最大值,且为8+
;
(2)椭圆的右准线为x=8,
离心率e=
=
,由椭圆的第二定义可得e=
(d为M到右准线的距离),
即有|MF2|=ed=
d,
|AM|+2|MF2|=|MA|+d,
过A作右准线的垂线,交点为P,由A,M,P共线,
可得|MP|为|AM|+2|MF2|的最小值,
且为8+2=10.
 (1)椭圆
(1)椭圆| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
焦点为F1(-2,0),F2(2,0),
由椭圆的第一定义可得|MF1|+|MF2|=2a=8,
|AM|+|MF2|=8+|MA|-|MF1|,
连接AF1,延长交椭圆于B,即有|BA|-|BF1|=|AF1|=
| 3 |
此时取得最大值,且为8+
| 3 |
(2)椭圆的右准线为x=8,
离心率e=
| c |
| a |
| 1 |
| 2 |
| |MF2| |
| d |
即有|MF2|=ed=
| 1 |
| 2 |
|AM|+2|MF2|=|MA|+d,
过A作右准线的垂线,交点为P,由A,M,P共线,
可得|MP|为|AM|+2|MF2|的最小值,
且为8+2=10.
看了 已知点A(-2,3)为椭圆x...的网友还看了以下:
已知圆柱形瓶A(底面半径25cm,高18cm)内装满水,圆柱形瓶B(底面半径31cm,高10cm) 2020-05-13 …
一个三角形,不是等腰.记这个三角形最长边的长度为a,最长的中线为c,最高的长度为b,请写出它们的大 2020-05-13 …
A盒内有一个黑球和三个白球,B盒内有两个白球和三个红球.若从A盒中随机抽取一球放入B盒内,然后又从 2020-06-16 …
若α平行β,a含于α,b含于β下列几种说法中正确的是①a平行b②a与β内无数条直线平行③a与β内的 2020-06-22 …
关于我国疆域的说法,正确的是()A.最北的省份是内蒙古自治区B.最东的省份是上海市C.最南的省份是 2020-07-04 …
唾液中的唾液淀粉酶进入胃后,失去活性,最佳解释是()A.胃内的温度高于口腔内的温度,蛋白质变性失活 2020-07-16 …
若α‖β,a包含于α,下列四个说法中正确的是1.a与β内所有直线平行2.a与β内的无数条直线平行3 2020-07-19 …
如图,在同一平面内两圆环A、B同心放置,A环中通以逆时针方向的恒定电流,关于穿过A、B两圆环的磁通 2020-07-31 …
设函数f(x)在区间(-a,a)(a>0)内为奇函数且可导,证明:f′(x)是(-a,a)内的偶函 2020-08-01 …
设f(x)为(a,b)内的初等函数,则下列命题正确的是()A、f(x)在(a,b)内一定可导B、f 2020-08-02 …