已知F1，F2分别为双曲线E：x2a2-y2b2=1（a>0，b>0）的左、右焦点，离心率为53，过原点的l交双曲线左、右两支分别于A，B，若|BF1|-|AF1|=6，则该双曲线的标准方程为（）A.x29-y216=1B.x218-y2

Question

已知F₁，F₂分别为双曲线E：

(x2)/(a2)-(y2)/(b2)=1（a>0，b>0）的左、右焦点，离心率为(5)/(3)，过原点的l交双曲线左、右两支分别于A，B，若|BF₁|-|AF₁|=6，则该双曲线的标准方程为（　　）

A.

(x2)/(9)-(y2)/(16)=1

B.

(x2)/(18)-(y2)/(32)=1

C.

(x2)/(9)-(y2)/(25)=1

D.

(x2)/(36)-(y2)/(64)=1

Answer 1

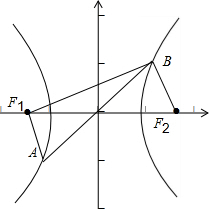根据题意，如图F₁，F₂分别为双曲线E的焦点，直线l交双曲线左、右两支分别于A，B，
直线l过原点，则直线l关于原点对称，则有|BF₂|=|AF₁|，
若|BF₁|-|AF₁|=6，则有|BF₁|-|BF₂|=6，
则双曲线E中，2a=6，即a=3，
又由双曲线E的离心率为(5)/(3)，即e=(c)/(a)=(5)/(3)，
则c=5，
b²=c²-a²=25-9=16；
则双曲线的方程为：(x2)/(9)-(y2)/(16)=1；
故选：A．