早教吧作业答案频道 -->数学-->
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是()A.1B.2C.32D.233
题目详情
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )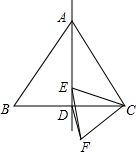
A. 1
B. 2
C. 3 2
D. 2 3 3
▼优质解答
答案和解析
如图所示:
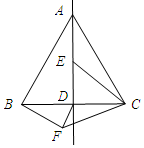
∵△ABC为等边三角形,AD是△ABC的高,
∴BD=
BC=
AB=2,∠EAC=
∠BAC=30°.
∵△ABC和△EFC都是等边三角形,
∴EC=CF,BC=AC,∠FCE=∠DCA.
∴∠FCE-∠DCE=∠DCA-∠DCE,即∠BCF=∠ACE.
在△BFC和△AEC中
,
∴△BFC≌△AEC.
∴∠FBC=∠EAC=30°.
由垂线段的性质可知:当DF⊥BF时,DF有最小值.
在Rt△BDF中,∠FBD=30°,BD=2,
∴DF=
BD=
×2=1.
∴DF的最小值为1.
故选:A.

∵△ABC为等边三角形,AD是△ABC的高,
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC和△EFC都是等边三角形,
∴EC=CF,BC=AC,∠FCE=∠DCA.
∴∠FCE-∠DCE=∠DCA-∠DCE,即∠BCF=∠ACE.
在△BFC和△AEC中
|
∴△BFC≌△AEC.
∴∠FBC=∠EAC=30°.
由垂线段的性质可知:当DF⊥BF时,DF有最小值.
在Rt△BDF中,∠FBD=30°,BD=2,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF的最小值为1.
故选:A.
看了 如图,△ABC和△EFC都是...的网友还看了以下:
已知抛物线y²=2px(p>0)的焦点恰好是椭圆a>b>0的右焦点F2且两条曲线的公共点的连线过F 2020-06-05 …
圆上的一点与一条直线距离最短时该点与直线连线过圆心为什么? 2020-07-26 …
谁能帮忙证下:过抛物线准线上任意一点做该抛物线的两条切线.证明:两切线互相垂直且切点连线过抛物线焦 2020-07-31 …
谁能帮忙证下:过抛物线准线上任意一点做该抛物线的两条切线.证明:两切线互相垂直且切点连线过抛物线焦 2020-07-31 …
谁能帮忙证下:过抛物线准线上任意一点做该抛物线的两条切线.证明:两切线互相垂直且切点连线过抛物线焦 2020-07-31 …
已知y2=2px,在准线上一点P,过P做抛物线两条切线,求证两个切点连线过焦点能不能不用导数 2020-07-31 …
已知抛物线y^2=2PX(P>0)焦点F恰好是双曲线X^2/a^2-y^2/b^2=1的右焦点,且两 2020-11-01 …
若抛物线C1:y2=4x的焦点F恰好是双曲线C2:x2a2-y2b2=1(a>0,b>0)的右焦点, 2020-11-03 …
高二数学---圆锥曲线已知抛物线x^2=2py(p>0)的焦点F恰好是双曲线y^2/a^2-x^2/ 2020-11-18 …
如图所示,水平圆盘上A、B两物块用弹簧相连,弹簧处于压缩状态,A、B连线过圆盘圆心.圆盘以角速度ω0 2020-12-05 …