已知三棱柱P-ABC的各顶点都在以O为球心的球面上，且PA、PB、PC两垂直，若PA=PB=PC=2，则球心O到平面ABC的距离为（）A.233B.3C.1D.33

Question

已知三棱柱P-ABC的各顶点都在以O为球心的球面上，且PA、PB、PC两垂直，若PA=PB=PC=2，则球心O到平面ABC的距离为（　　）

A.

(2√(3))/(3)

B.

√(3)

C. 1

D.

(√(3))/(3)

Answer 1

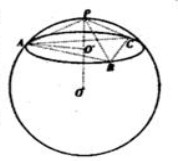如图，设过A，B，C的截面圆的圆心为O′，半径为r，球心O到该截面的距离为d，
因为PA，PB，PC两两垂直，且PA=PB=PC=2，
所以AB=BC=CA=2√(2)，且O′为△ABC的中心，
于是(2√(2))/(sin60°)=2r，得r=(2√(6))/(3)，
又PO′=√(4-r2)=(2√(3))/(3)．
OO′=R-(2√(3))/(3)=d=√(R2-r2)，解得R=√(3)，
故d=R-(2√(3))/(3)=(√(3))/(3)．
故选：D．