已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BD⊥AD,且AD=25,BD=2,CD=3,则球O的体积为()A.86πB.273π2C.77π6D.103π
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BD⊥AD,且AD=2
,BD=2,CD=5
,则球O的体积为( )3 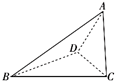
A. 8
π6
B. 27
π3 2
C. 7
π7 6
D. 10
π3
∴AC⊥BD,
∵BD⊥AD,AC∩AD=A,
∴BD⊥平面ACD,
∴三棱锥S-ABC可以扩充为以AB为对角线的长方体,外接球的直径为AB,
∴4R2=AB2=BD2+AD2=4+20=24,
∴R=
| 6 |
∴球O的体积为
| 4 |
| 3 |
| 6 |
故选:A.
将三角形ade绕点a按顺时针转动,使点d落在线段ab上,其他条件不变如图1所示,三角形ABC与三角 2020-04-11 …
如图,在楼AB与楼CD之间有一旗杆EF,从AB顶部A点处经过旗杆顶部E点恰好看到楼CD的底部D点, 2020-05-17 …
已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线 2020-07-09 …
如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是()A.线段CD的中点B.OA与OB的 2020-07-24 …
如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是()A.线段CD的中点B.OA与OB的 2020-07-29 …
如图,在△ABC中,∠ACB=90°,D是AB的中点,CD=3,过点A作∠CAE=∠B,交边CB于点 2020-11-01 …
如图:点D在线段AB的延长线上,把AB绕点A逆时针旋转90°得到AC,连接CD,点E在CD上,BF∥ 2020-11-03 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
,AB为弧形光滑轨道,CD是一半为R的竖直放置的半圆形光滑轨道,D点在C点AB为弧形光滑轨道,CD是 2020-12-25 …
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的 2021-01-05 …