早教吧作业答案频道 -->数学-->
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c的顶点,则方程x2+bx+c=1的解的个数是()A.0或2B.0或1C.1或2D.0,1,或2
题目详情
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=x2+bx+c的顶点,则方程x2+bx+c=1的解的个数是( )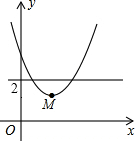
A. 0或2
B. 0或1
C. 1或2
D. 0,1,或2
▼优质解答
答案和解析
由抛物线y=x2+bx+c的图象可知,该抛物线与x轴没有交点
即:△<0
则:b2-4c<0
又点M是直线y=2与x轴之间的一个动点,点M的坐标为:(-
,
)
所以,0<
<2
0<4c-b2<8,
-8<b2-4c<0,
令y=x2+bx+c-1,则要求方程x2+bx+c=1的解得个数,只需判定抛物线y=x2+bx+c-1与x轴有无交点及交点的个数即可.
又因为,△=b2-4ac=b2-4(c-1)=b2-4c+4
所以,-4<b2-4c+4<4
即:①当-4<b2-4c+4<0时,抛物线y=x2+bx+c-1与x轴没有交点;
②b2-4c+4=0时,抛物线y=x2+bx+c-1与x轴有一个交点;
③0<b2-4c+4<4时,抛物线y=x2+bx+c-1与x轴有两个交点.
故:选D
即:△<0
则:b2-4c<0
又点M是直线y=2与x轴之间的一个动点,点M的坐标为:(-
| b |
| 2 |
| 4c-b2 |
| 4 |
所以,0<
| 4c-b2 |
| 4 |
0<4c-b2<8,
-8<b2-4c<0,
令y=x2+bx+c-1,则要求方程x2+bx+c=1的解得个数,只需判定抛物线y=x2+bx+c-1与x轴有无交点及交点的个数即可.
又因为,△=b2-4ac=b2-4(c-1)=b2-4c+4
所以,-4<b2-4c+4<4
即:①当-4<b2-4c+4<0时,抛物线y=x2+bx+c-1与x轴没有交点;
②b2-4c+4=0时,抛物线y=x2+bx+c-1与x轴有一个交点;
③0<b2-4c+4<4时,抛物线y=x2+bx+c-1与x轴有两个交点.
故:选D
看了 如图,平面直角坐标系中,点M...的网友还看了以下:
已知A={X∈R|X^2-2X-8=0},B={X∈R|X^2+aX+a^2-12=0},B是A的 2020-04-25 …
(b-c)^2=(c-a)^2=(a-b)^2求证:a=b=c(b-c)^2-(c-a)^2=0( 2020-04-26 …
下列四种烃的名称所表示的物质,命名正确的是A.2-甲基-2-丁炔B.2-乙基丙烷C.3-甲基-2- 2020-05-02 …
|a|>2是a>2的什么条件 2020-05-15 …
若a加b分之a减b等于三,求代数式a加b分之2(a减b)减3(a减b)分之4(a加b)的值 请尽快 2020-05-16 …
设a,b为非零向量,|b|=2|a|,两组向量x1,x2,x3,x4和y1,y2,y3,y4均由2 2020-05-17 …
f(x)=x^2+|x-a|+1,x属于R,常数a为R,求f(x)最小值x=a再分别讨论a的取值情 2020-05-23 …
已知三角形的三个顶点分别为A(6,-7),B(-2,3),C(2,1),求AC边上的中线所在的直线 2020-06-03 …
二次函数的问题,有难度已知抛物线Y=X^2+AX+A-2设Y=X^2+AX+A-2与Y轴交点C,如 2020-06-13 …
不等式(2-a)x2-2(a-2)x+4>0对于一切实数x都成立,则()A.{a|-2<a<2}B 2020-06-15 …