早教吧作业答案频道 -->数学-->
如图,O是△ABC内一点,O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.(1)求证:AB=AC.(2)已知AB=10,BC=12,求四边形DFGE是矩形时O的半径.
题目详情
如图,O是△ABC内一点, O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.
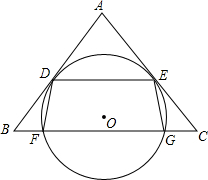
(1)求证:AB=AC.
(2)已知AB=10,BC=12,求四边形DFGE是矩形时 O的半径.

(1)求证:AB=AC.
(2)已知AB=10,BC=12,求四边形DFGE是矩形时 O的半径.
▼优质解答
答案和解析
(1)证明:∵AD、AE是 O的切线,
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2) 如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设 O半径为r,
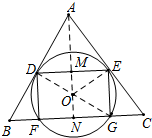
∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是 O直径,
∵ O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=
BC=6,
在RT△ABN中,AN=
=
=8,
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴
=
,即
=
,
∴AD=
r,
∴BD=AB-AD=10-
r,
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴
=
,即
=
,
∴r=
,
∴四边形DFGE是矩形时 O的半径为
.
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2) 如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设 O半径为r,

∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是 O直径,
∵ O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=
| 1 |
| 2 |
在RT△ABN中,AN=
| AB2-BN2 |
| 102-62 |
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴
| OD |
| BN |
| AD |
| AN |
| r |
| 6 |
| AD |
| 8 |
∴AD=
| 4 |
| 3 |
∴BD=AB-AD=10-
| 4 |
| 3 |
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴
| BD |
| BN |
| GD |
| AN |
10-
| ||
| 6 |
| 2r |
| 8 |
∴r=
| 60 |
| 17 |
∴四边形DFGE是矩形时 O的半径为
| 60 |
| 17 |
看了 如图,O是△ABC内一点,O...的网友还看了以下:
已知向量a=﹙﹣2,sina﹚,向量b=﹙cosa,1﹚,a∈‐π∕3,π∕61、是否存在a,是向 2020-05-22 …
初三数学二次根式(1)若m,n为一等腰△的两边之长,且满足等式2根号(3m-6)+3根号(2-m) 2020-06-06 …
已知a²(b+c)=b²(a+c)=2010且a≠b.求c²(a+b)的值 2020-06-12 …
设f(x),g(x)在[a,b]上连续,且均为严格单增的正函数,证明:存在c€(a,b)使f(b) 2020-06-18 …
在三角形ABC中,角A,B,C对应边分别为a,b,c,且象量AB点乘AC=BA点乘BC=1,求证角 2020-07-08 …
数学向量内积,只用求b出来就行.数学向量内积已知a=(3,4),b是与a垂直的单位向量,c=a-b 2020-07-22 …
设G是一个非空集合,*是定义在G上的一个运算.如果同时满足下述四个条件:(ⅰ)对于∀a,b∈G,都 2020-08-01 …
非空集合G关于运算⊕满足:(1)对任意的a,b∈G,都有a⊕b∈G;(2)存在e∈G,都有a⊕e= 2020-08-01 …
在矩形ABCD中,边长AB=3,AD=4,两动点E,F分别从顶点B,C同时开始以相同速度在边BC, 2020-08-02 …
(2009•宜宾)A、B、C、D、E、F、G是常见的七种物质,A是含有两种元素的固体化合物,C是一切 2020-11-12 …