如图，在平面直角坐标系中，点A坐标为（6，0），在B在y轴的正半轴上，且S△AOB=24．（1）求点B坐标；（2）若点P从B出发沿y轴负半轴运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，

Question

如图，在平面直角坐标系中，点A坐标为（6，0），在B在y轴的正半轴上，且S_△AOB=24．
（1）求点B坐标；
（2）若点P从B出发沿y轴负半轴运动，速度每秒2个单位，运动时间t秒，△AOP的面积为S，求S与t的关系式，并直接写出t的取值范围；
（3）在（2）的条件下，若S_△AOP：S_△ABP=1：3，且S_△AOP+S_△ABP=S_△AOB，在线段AB的垂直平分线上是否存在点Q，使得△AOQ的面积与△BPQ的面积相等？若存在，求出Q点坐标；若不存在，请说明理由．

Answer 1

（1）∵点A坐标为（6，0），
∴OA=6，
∴S_△AOB=(1)/(2)×OA×OB=24，
则OB=8，
∴点B坐标为（0，8）；
（2）当0≤t<4时，S=(1)/(2)×（8-2t）×6=24-6t，
当t≥4时，S=(1)/(2)×（2t-8）×6=6t-24；
（3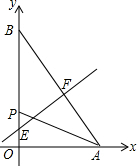）∵S_△AOP+S_△ABP=S_△AOB，
∴点P在线段OB上，
∵S_△AOP：S_△ABP=1：3，
∴OP：BP=1：3，
又∵OB=8，
∴OP=2，BP=6，
线段AB的垂直平分线上交OB于E，交AB于F，
∵OB=8，OA=6，
∴AB=√(OB2+OA2)=10，
则点F的坐标为（3，4），
∵EF⊥AB，∠AOB=90°，
∴△BEF∽△BAO，
∴(BE)/(BA)=(BF)/(BO)，即(BE)/(10)=(5)/(8)，
解得，BE=(25)/(4)，
则OE=8-(25)/(4)=(7)/(4)，
∴点E的坐标为（0，(7)/(4)），
设直线EF的解析式为y=kx+b，
则

3k+b=4

b=(7)/(4)

，
解得，k=(3)/(4)，b=(7)/(4)，
∴直线EF的解析式为y=(3)/(4)x+(7)/(4)，
∵△AOQ的面积与△BPQ的面积相等，又OA=BP，
∴x=y，或x=-y，
当x=y时，x=(3)/(4)x+(7)/(4)，解得，x=7，
则Q点坐标为（7，7）；
当x=-y时，-x=(3)/(4)x+(7)/(4)，解得，x=-1，
则Q点坐标为（-1，1），
∴Q点坐标为（7，7）或（-1，1）．