早教吧作业答案频道 -->数学-->
已知四边形ABCD内接于O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30
题目详情
已知四边形ABCD内接于 O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与 O的位置关系,并说明理由.
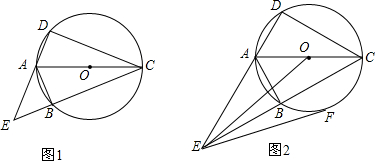
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与 O的位置关系,并说明理由.

▼优质解答
答案和解析
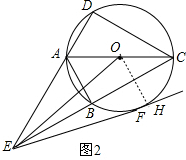 (1)证明:∵对角线AC平分∠DCB,
(1)证明:∵对角线AC平分∠DCB,
∴∠ACD=∠ACB,
∴
=
,
∴AD=AB,
∵EB=AD,
∴AB=EB,
∵∠EBA=∠ADC=90°,
∴△ABE是等腰直角三角形
(2) 直线EF与 O相离.理由如下:
∵∠DCB<90°,∠ACD=∠ACB,
∵∠ACE≥30°,
∴60°≤∠DCE<90°,
∴∠AEC≤30°,
∴AE≥AC,
∵OE>AE,
∴OE>AC,
作OH⊥EF于H,如图,
在Rt△OEH中,∵∠OEF=30°,
∴OH=
OE,
∴OH>OA,
∴直线EF与 O相离.
 (1)证明:∵对角线AC平分∠DCB,
(1)证明:∵对角线AC平分∠DCB,∴∠ACD=∠ACB,
∴
 |
| AD |
 |
| AB |
∴AD=AB,
∵EB=AD,
∴AB=EB,
∵∠EBA=∠ADC=90°,
∴△ABE是等腰直角三角形
(2) 直线EF与 O相离.理由如下:
∵∠DCB<90°,∠ACD=∠ACB,
∵∠ACE≥30°,
∴60°≤∠DCE<90°,
∴∠AEC≤30°,
∴AE≥AC,
∵OE>AE,
∴OE>AC,
作OH⊥EF于H,如图,
在Rt△OEH中,∵∠OEF=30°,
∴OH=
| 1 |
| 2 |
∴OH>OA,
∴直线EF与 O相离.
看了 已知四边形ABCD内接于O,...的网友还看了以下:
矩形ABCD中,0是对角线AB与BD的交点,过点0的直线EF分别交AB、CD的延长线于EF.求:当 2020-04-09 …
将一个正方形延对角线方向.将一个正方形延对角线方向连续平移三次得一个由四个正方形组成的图形,应怎样 2020-06-12 …
如图,△ABC为等边三角形,延长BC到D,延长BA到E,AE=BD,连接EC,ED,求证:三角形D 2020-06-27 …
在三角形中,A和B满足关系式1/tanAtanB>0,此三角形的形状是A锐角三角形B钝在三角形中, 2020-06-29 …
在等腰直角三角形三角形ABC中,AB垂直BC.AB=BC.延长CB至E(向B方向延),在AB边上取 2020-07-25 …
有关于三角形三角形到底是由三条直线组成的还是由三条线段组成的?一个三角形有几个同旁内角?如果三角形 2020-07-29 …
若三角形ABC为正三角形,延长BC至E,延长CB至D,使角DAE等于120度,试说明BC等于BD与 2020-07-30 …
一个多边形截去一个角后,形成一个新多边形,新多边形内角和是2520度,则原多边形边数是多少?2延长 2020-08-02 …
如图,三角形ABC是边长为2cm的等边三角形,延长CB到D,使BD=CB,延长BC到E,使CE=CB 2020-11-28 …
叙述一下图形:一个正方形延长一条边联结上边的一点,使图形形状是一个正方形加一个直角三角形的样子已知: 2020-12-07 …