如图，AB是圆O的直径，PA垂直于圆O所在的平面，M是圆周上任意一点，AN⊥PM，垂足为N．求证：AN⊥平面PBM．

Question

如图，AB是圆O的直径，PA垂直于圆O所在的平面，M是圆周上任意一点，AN⊥PM，垂足为N．

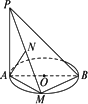
求证：AN⊥平面PBM．

Answer 1

答案：

解析：

　　证明：设圆O所的在平面为α，则已知PA⊥α，且BM α，

　　∴PA⊥BM．又∵AB为⊙O的直径，点M为圆周上一点，

　　∴AM⊥BM．由于直线PA∩AM＝A，

　　∴BM⊥平面PAM．

　　而AN 平面PAM，∴BM⊥AN．

　　这样，AN与PM、BM两条相交直线垂直．

　　故AN⊥平面PBM．

　　方法归纳：直线垂直于平面，则必垂直于平面内的任意一条直线．要证直线垂直于平面，必须证明直线垂直于平面内的两条相交直线．

提示：

要证线面垂直，需证直线和平面内的两条相交直线都垂直．已知AN⊥PM，只需再证AN和平面PBM内的另一条直线，如BM或PB垂直即可．再结合已知中线面垂直，可找线线垂直．